2. PEATÜKK. AATOMITE KVANTMEHAANIKA
§ 1. Vesinikusarnase aatomi teooria
Aatomite ja molekulide Schrödingeri võrrandi lahendamisel saadud lainefunktsioonide kuju on üldjuhul erakordselt keerukas. Aatomite korral lihtsustab vaatlust mõnevõrra asjaolu, et tegemist on vaid ühe tuumaga. Seetõttu tuleb süsteemi kirjeldamisel vaadelda ainult elektronide liikumist ümber koordinaatide alguspunkti fikseeritud tuuma. Üheelektroonsed lainefunktsioonid, mis kirjeldavad seda elektronide liikumist, kannavad aatomorbitalid IPM-mudeli kasutamise tõttu (vt. 1 ptk. § 8) leitavad vaid ligikaudselt.
Alustame vaatlust lihtsamatest aatomitest, mis koosnevad vaid aatomituumast ning ühest elektronist. Sellisteks aatomiteks on ![]() jne. ning neid nimetatakse vesinikusarnasteks aatomiteks. Selliste aatomite korral on kogu lainefunktsioon samane elektroni lainefunktsiooniga. Jättes kõrvale mitmeid suurusjärke väiksemad magnetilised vastasmõjud elementaarosakeste vahel, on meil tegemist ühe negatiivselt laetud elektroniga aatomituuma elektrostaatilises tsentraalsümmeetrilises väljas. Selle, nn. Kepleri süsteemi Schrödingeri võrrand on täpselt lahenduv.
jne. ning neid nimetatakse vesinikusarnasteks aatomiteks. Selliste aatomite korral on kogu lainefunktsioon samane elektroni lainefunktsiooniga. Jättes kõrvale mitmeid suurusjärke väiksemad magnetilised vastasmõjud elementaarosakeste vahel, on meil tegemist ühe negatiivselt laetud elektroniga aatomituuma elektrostaatilises tsentraalsümmeetrilises väljas. Selle, nn. Kepleri süsteemi Schrödingeri võrrand on täpselt lahenduv.
Tuumalaengut Z omava vesinikusarnase aatomi Schrödingeri võrrand avaldub ristkoordinaatides kujul* :
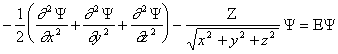 .
.
(2.1)
Selle diferentsiaalvõrrandi otsest lahendamist takistab elektroni koordinaatide ruutude summa ruutjuure märgi all potentsiaalse energia liikmes. Tekkinud raskusest saadakse üle sobiva koordinaatide süsteemi valikuga. Tsentraalsümmeetrilise välja probleemide lahendamisel kasutatakse sfäärilisi koordinaate ![]() (vt. joonis 2).
(vt. joonis 2).
Aatomiühikute süsteem
|
Füüsikaline suurus |
Tähis |
Definitsioon |
Seos SI-süsteemi mõõtühikuga |
|
Mass |
|
elektroni mass |
9,109534 · 10 -31kg |
|
Pikkus |
(bohr) |
elektroni Bohri orbiidi raadius |
5,2917706 · 10- 11m |
|
H aatomis |
|||
|
Laeng |
|
elektroni laeng |
1,6021892 ·10 -19C |
|
Aeg |
|
|
2,419 · 10 -17C |
|
Plancki konstant |
|
|
1,055 · 10 -34J · s |
|
Energia |
|
H aatomi ionisat- sioonipotentsiaali kahekordne väärtus |
4,3598144 · 10 -18J |
|
Molaarne energia |
|
|
2625,500 kJ/mol |
|
Dipoolmoment |
|
|
8,4784 · 10 -30C · m |
|
Kvadrupoolmo-ment |
|
|
4,4866 · 10 -40C · m2 |
|
Elektriväli |
|
|
5,1423 · 10 11Vm-1 |
Joonis 2
Sfäärilised koordinadid (r-raadius, ![]() -sfäärilised nurgad).
-sfäärilised nurgad).
Rist- ja sfäärilised koordinaadid on omavahel seotud järgmiste suhetega:
![]() (2.2a)
(2.2a)
![]() (2.2b)
(2.2b)
![]() (2.2c)
(2.2c)
Seejuures
![]()
Schrödingeri võrrandis olev elektroni kineetilise energia diferentsiaaloperaator avaldub sfäärilistes koordinaatides kujul:
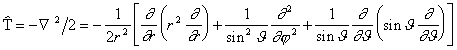 .
.
(2.3)
Oluliselt lihtsustub potentsiaalse energia operaator:
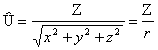 .
.
(2.4)
Seega on vesinikusarnase aatomi Schrödingeri võrrand sfäärilistes koordinaatides kujul:
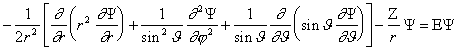 .
.
(2.5)
Esimesel pilgul näib võrrand olevat muutunud isegi keerulisemaks, kuid tegelikult on nüüd võimalik muutujate eraldamine. Otsime lahendit, elektroni lainefunktsiooni, kujul
![]() ,
,
(2.6)
s.o. ainult raadiuskoordinaadist sõltuva radiaalosa ![]() ning sfäärilistest nurkadest
ning sfäärilistest nurkadest ![]() sõltuva sfäärilise osa
sõltuva sfäärilise osa ![]() korrutisena. Asendades viimase avaldise võrrandisse (2.5) ning korrutades siis selle mõlemaid pooli suurusega
korrutisena. Asendades viimase avaldise võrrandisse (2.5) ning korrutades siis selle mõlemaid pooli suurusega
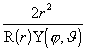 ,
,
on lihtne eraldada muutujad:
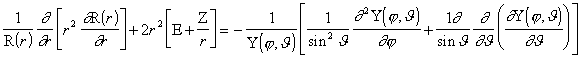
(2.7)
Kuna viimase võrrandi mõlemad pooled sisaldavad omavahel sõltumatuid muutujaid, siis kehtib ta vaid juhul, kui mõlemad pooled on võrdsed mingi arvulise konstandiga ![]() . Järelikult võime välja kirjutada kaks sõltumatut diferentsiaalvõrrandit (jättes märkimata funktsioonide R ja Y muutujad):
. Järelikult võime välja kirjutada kaks sõltumatut diferentsiaalvõrrandit (jättes märkimata funktsioonide R ja Y muutujad):
![]()
(2.8a)
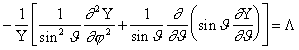
(2.8b)
Saadud võrrandite lahendamine on matemaatiliselt küllaltki töömahukas ning seetõttu esitame siinkohal vaid lahendid
*.Sfäärilisi muutujaid sisaldava diferentsiaalvõrrandi (2.8b) lahenditeks on sfäärilised harmoonikud:
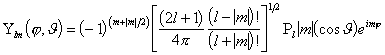 ,
,
(2.9)
kus
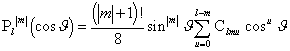
(2.10)
on Legendre'i kaaspolünoomid. Konstandid ![]() tähistavad viimases võrrandis polünomiaalkordajaid. Sfäärilised harmoonikud sõltuvad kahest kvantarvust. Orbitaalne e. asimutaalne kvantarv l võib omada väärtusi
tähistavad viimases võrrandis polünomiaalkordajaid. Sfäärilised harmoonikud sõltuvad kahest kvantarvust. Orbitaalne e. asimutaalne kvantarv l võib omada väärtusi
![]()
ning magnetiline kvantarv m väärtusi
![]() .
.
Sfäärilised harmoonikud madalamate l väärtuste korral on toodud tabelis 3.
Vesinikusarnase aatomi ülesande radiaalse osa (2.8a) lahendid on kujul
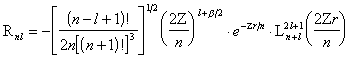 ,
,
(2.11)
kus
![]()
(2.12)
on Laguerre'i kaaspolünoomid. Radiaalsed lainefunktsioonid ![]() sõltuvad lisaks orbitaalsele kvantarvule l veel peakvantarvust n, mille võimalikud väärtused on
sõltuvad lisaks orbitaalsele kvantarvule l veel peakvantarvust n, mille võimalikud väärtused on
![]()
Radiaalsete funktsioonide kuju mõnede n ja l kombinatsioonide korral on toodud tabelis 4.
Radiaalse võrrandi (2.8a) lahendamisel saab ka energia väärtuse:
![]() ,
,
(2.13)
kus n on jällegi peakvantarv. Tegemist on vesinikusarnase aatomi energiaga selle peakvantarvuga määratud olekus. Seega on vesinikusarnase aatomi koguenergia vaid ühe kvantarvu (n) funktsioon.
§ 2. Aatomorbitalide kuju
Vesinikusarnase aatomi orbitalidega on sarnased ka mitut elektroni sisaldavate aatomite üheelektroonsed lainefunktsioonid. Aaatomorbitalide kuju ning nende omadused mitmesuguste sümmeetriaoperatsioonide suhtes määravad aga neist moodustunud keemiliste sidemete iseloomu ja tüübi.
Aatomorbitalid (lühendatult AO-d) ![]() on põhimõtteliselt kahe erinevatest ruumikoordinaatidest sõltuva funktsiooni korrutised:
on põhimõtteliselt kahe erinevatest ruumikoordinaatidest sõltuva funktsiooni korrutised:
![]() .
.
(2.14)
Mistahes aatomorbitaali korral kujutab sfäärilistest nurgakoordinaatidest sõltuv osa ![]() endast sfäärilist harmoonikut (vt. 2.9), mida omakorda võib vaadelda kahe sõltumatu funktsiooni korrutisena
endast sfäärilist harmoonikut (vt. 2.9), mida omakorda võib vaadelda kahe sõltumatu funktsiooni korrutisena
![]()
(2.15)
Sfäärilisi harmoonikuid võib rühmitada vastavalt orbitaalse kvantarvu l väärtusele. Viimane määrab ära funktsiooni ![]() nulltasandite arvu muutumispiirkonnas
nulltasandite arvu muutumispiirkonnas ![]() . Sfäärilisel harmoonikul kvantarvuga
. Sfäärilisel harmoonikul kvantarvuga ![]() puudub seega nulltasand ning sõltumatult nurkadest
puudub seega nulltasand ning sõltumatult nurkadest ![]() omab ta konstantset väärtust antud raadiuskoordinaadi r korral. Taolist funktsiooni iseloomustab sfääriline sümmeetria (vt. joonis 3).
omab ta konstantset väärtust antud raadiuskoordinaadi r korral. Taolist funktsiooni iseloomustab sfääriline sümmeetria (vt. joonis 3).
Orbitaalse kvantarvuga l = 1 on kolm sfäärilist harmoonikut (vt. tabel 30. Vaatleme näiteks funktsiooni ![]()
![]()
![]() . Kuna alati
. Kuna alati ![]() , siis on sellel funktsioonil vastavalt muutuja z väärtusele kaks erineva märgiga iseloomustatud piirkonda. Kui
, siis on sellel funktsioonil vastavalt muutuja z väärtusele kaks erineva märgiga iseloomustatud piirkonda. Kui ![]() , siis ka
, siis ka ![]() ning kui
ning kui ![]() , siis
, siis ![]() . Võrrandiga
. Võrrandiga
![]()
(2.16)
määratud tasandis on ka sfääriline harmoonik ![]() , s.t. see ongi nulltasand.
, s.t. see ongi nulltasand.
Funktsiooni ![]() arvuline väärtus on kogu muutumispiirkonnas oluliselt määratud funktsiooniga
arvuline väärtus on kogu muutumispiirkonnas oluliselt määratud funktsiooniga ![]()
![]() :
:
![]()
(vt. tabel 3). Joonisel 3 on näha, et vastavalt koosinusfunktsiooni väärtusele saame kahe sfääri kujutise, millest üks on määratud positiivsete, teine aga negatiivsete z väärtuste piirkonnas.
Analoogiliselt võib analüüsida ka sfäärilisi harmoonikuid ![]()
![]() . Seejuures ilmneb, et nende kuju on identne funktsiooni
. Seejuures ilmneb, et nende kuju on identne funktsiooni ![]() kujuga. Kuid nad on orienteeritud vastavalt x- ja y-telje suunas (vt. joonis 3).
kujuga. Kuid nad on orienteeritud vastavalt x- ja y-telje suunas (vt. joonis 3).
Mõnevõrra keerukam on orbitaalsele kvantarvule l=2 vastavate sfääriliste harmoonikute analüüs. Nende geomeetrilised kujud on toodud samuti joonisel 3.
Märgime veelkord, et aatomorbitalide sfäärilised osad on universaalsed, s.t. nad ei sõltu aatomi tüübist. Antud H-sarnasele aatomile spetsiifilised on aga aatomorbitalide radiaalsed osad ![]() . Viimased on täpsel analüütilisel kujul esitatavad vaid vesinikusarnaste aatomite korral. Mitme elektroniga aatomite korral saab lahendeid leida vaid Schrödingeri võrrandi numbrilise integreerimise või ligikaudse rittaarenduse teel. Saadud funktsioonid on oma omadustelt siiski väga lähedased vesinikusarnase aatomi orbitalide radiaalse osaga. Viimaseid võib vaadelda üldkujul
. Viimased on täpsel analüütilisel kujul esitatavad vaid vesinikusarnaste aatomite korral. Mitme elektroniga aatomite korral saab lahendeid leida vaid Schrödingeri võrrandi numbrilise integreerimise või ligikaudse rittaarenduse teel. Saadud funktsioonid on oma omadustelt siiski väga lähedased vesinikusarnase aatomi orbitalide radiaalse osaga. Viimaseid võib vaadelda üldkujul
![]() ,
,
(2.17)
kus![]() on
on ![]() -astme polünoom muutujast r. Kuivõrd eksponentfunktsioon kahaneb kiiremini mistahes polünoomi kasvust, on garanteeritud piirtingimus
-astme polünoom muutujast r. Kuivõrd eksponentfunktsioon kahaneb kiiremini mistahes polünoomi kasvust, on garanteeritud piirtingimus
![]() .
.
(2.18)
Seega on elektroni esinemise tõenäosus suurem väikeste r väärtuste korral (tuuma ligidal).
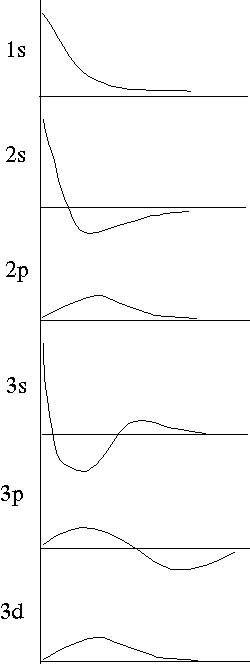
Joonisel 4 on lihtsamate juhtude jaoks toodud funktsiooni ![]() , elektroni leidmise tõenäosuse tiheduse
, elektroni leidmise tõenäosuse tiheduse ![]() ja elektroni leidmise tõenäosuse
ja elektroni leidmise tõenäosuse ![]() sõltuvus kaugusest tuumast. Näeme, et ka lainefunktsiooni radiaalne osa võib omada nullkohti vahemikus
sõltuvus kaugusest tuumast. Näeme, et ka lainefunktsiooni radiaalne osa võib omada nullkohti vahemikus ![]() . Nende arv
. Nende arv ![]() on määratud kvantarvudega n ja l:
on määratud kvantarvudega n ja l:
![]() .
.
(2.19)
Tabel 3
Normeeritud sfäärilised harmoonikud
_________________________________________________________________
Sfääriline harmoonik
l m Tähistus sfäärilistes koordinaatides ristkoordinaatides
_________________________________________________________________
|
0 |
0 |
s |
|
|
|
1 |
0 |
|
|
|
|
1 |
-1 |
|
|
|
|
1 |
1 |
|
|
|
|
2 |
0 |
|
|
|
|
2 |
-1 |
|
|
|
Tabel 4
Vesinikusarnase aatomi lainefunktsiooni
radiaalne osa ![]() (suurus
(suurus ![]() )
)
_________________________________________________________________
n l Tähistus ![]()
_________________________________________________________________
|
1 |
0 |
1s |
|
|
2 |
0 |
2s |
|
|
2 |
1 |
2p |
|
|
3 |
0 |
3s |
|
|
3 |
1 |
3p |
|
|
3 |
2 |
3d |
|
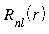
|
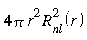
|
|---|---|
|
|
Joonis 4. Aatomorbitalide sfäärilise osa sõltuvus kaugusest tuumast.

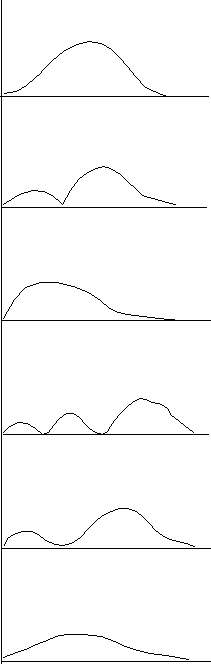
Joonis 5. Aatomorbitalide radiaalse osa kontuurkaardid.
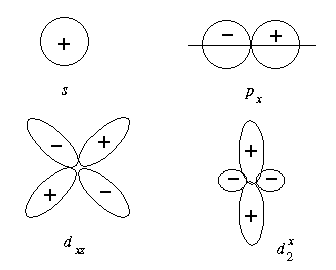
Joonis 6. Mõnede aatomorbitalide polaarsed diagrammid.
![]()
Keemilise sideme tekkemehanismi mudelite uurimisel on oluliseks aatomi lainefunktsiooni suurus ja märk ühes või teises ruumipiirkonnas. Selle piltlikuks esitamiseks kasutatakse kas radiaalsete funktsioonide kontuurkaarte (vt. joonis 5) või skemaatilisi polaarseid diagramme (joonis 6).
Iga AO on tähistatud sümboliga, mis koosneb tema peakvantarvust ning orbitaalsele kvantarvule l vastavast tähelisest indeksist. Seejuures kehtib järgmine vastavus:
l väärtus: 0 1 2 3 4
täheline indeks: s p d f g
Seega on n ja l kasvades järjestikused AO-d tähistatud sümbolitega 1s, 2s, 2p, 3s, 3p, 3d, 4s jne.
§ 3. Mitme elektroniga aatomi elektroonse lainefunktsiooni leidmine
Mitut elektroni sisaldava aatomi korral avaldab antud elektroni liikumisele mõju ka teiste elektronide elektrostaatiline väli ning seetõttu pole tema jaoks enam tegemist lihtsa tsentraalvälja potentsiaaliga. Matemaatiliselt avaldub selline potentsiaal valemiga:
![]() ,
,
(2.20)
kus ![]() on elektroni kaugus tuumast ja
on elektroni kaugus tuumast ja ![]() tema kaugus teistest elektronidest.
tema kaugus teistest elektronidest.
Järgnevalt kirjeldame kahte sümboolset operatsiooni, mis viivad matemaatilise aparaadi suurele lihtsustusele ning võimaldavad defineerida orbitali mõiste paljuelektroonses aatomis.
Esiteks leiame formaalselt elektronide tõukumise keskväärtuse üle kõigi ülejäänud elektronide i (antud elektroni jaoks). Tulemuseks saame
![]() ,
,
(2.21)
s.o. 1. elektroni raadiusvektorist ![]() sõltuva potentsiaali. See potentsiaal pole tingimata sfäärilise sümmeetriaga, kuna 1. elektron ise võib omada juhuslikku asendit ruumis. Seetõttu tuleb leida veel potentsiaali
sõltuva potentsiaali. See potentsiaal pole tingimata sfäärilise sümmeetriaga, kuna 1. elektron ise võib omada juhuslikku asendit ruumis. Seetõttu tuleb leida veel potentsiaali
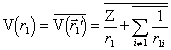 .
.
(2.22)
Viimane potentsiaal on juba sfäärsümmeetriline ning seetõttu on temale vastava Schrödingeri võrrandi
![]()
(2.23)
lahendid esitatavad sõltumatute radiaalse ja sfäärilise osa korrutisena;
![]() .
.
(2.24)
Lahendid pole vaatamata lihtsustustele siiski leitavad analüütilisel kujul. Põhimõtteliselt suvalise täpsusega võib neid leida aga eespool kirjeldatud lähendusprotseduuri abil, kasutades nn. kooskõlalise välja (SCF) meetodit.
Probleemiks ei ole siin niivõrd keskväärtuste eneste leidmise protseduur, vaid see, et antud elektroni orbitali ![]() leidmiseks on kõigepealt vaja leida teiste elektronide tekitatud keskmine potentsiaal. Viimane sõltub muidugi nende ruumilisest jaotusest, s.t. nende orbitalidest
leidmiseks on kõigepealt vaja leida teiste elektronide tekitatud keskmine potentsiaal. Viimane sõltub muidugi nende ruumilisest jaotusest, s.t. nende orbitalidest ![]() , mille leidmisel on vaja eelnevalt teada ka orbitalil
, mille leidmisel on vaja eelnevalt teada ka orbitalil ![]() oleva elektroni tekitatud välja potentsiaali. Suletud ringist väljapääs peitub alljärgneva SCF protseduuri kasutamises:
oleva elektroni tekitatud välja potentsiaali. Suletud ringist väljapääs peitub alljärgneva SCF protseduuri kasutamises:
1. Valitakse mingisugused lähendusfunktsioonid ![]() iga elektroni orbitali jaoks (näiteks H-sarnased orbitalid).
iga elektroni orbitali jaoks (näiteks H-sarnased orbitalid).
2. Lähtudes neist orbitalidest määratakse vastavalt valemile (2.22) keskväärtustatud potentsiaal ![]() iga elektroni jaoks.
iga elektroni jaoks.
3. Saadud potentsiaal asendatakse üheelektroonsetesse võrranditesse (2.23) ning nende lahendamisel saadakse uus orbitalide komplekt ![]() .
.
4. Vastavalt Pauli printsiibile paigutatakse elektronid saadud orbitalidele ning arvutatakse uued potentsiaalid ![]() .
.
5. Võrreldakse antud k-ndal iteratsioonisammul saadud potentsiaale ![]() eelneval iteratsioonil kasutatud potentsiaalidega. Juhul kui potentsiaalid on jäänud praktiliselt muutumatuks, lõpetatakse protseduur ning tulemusena saadud viimased orbitalid ongi kooskõlalised e. Hartree-Focki SCF orbitalid. Vastasel korral jätkatakse iteratsiooni alates punktist 3.
eelneval iteratsioonil kasutatud potentsiaalidega. Juhul kui potentsiaalid on jäänud praktiliselt muutumatuks, lõpetatakse protseduur ning tulemusena saadud viimased orbitalid ongi kooskõlalised e. Hartree-Focki SCF orbitalid. Vastasel korral jätkatakse iteratsiooni alates punktist 3.
Oma kujult on aatomite SCF orbitalid sarnased H-sarnaste aatomite orbitalidega. Muuhulgas on ka nende sfääriliste ja radiaalsete sõlmpindade arvud võrdsed ning määratud kvantarvudega n ja l.
§ 4. He aatomi ülesanne
Leiame variatsioonimeetodil lihtsaima kaheelektroonse aatomi -He energia ja lainefunktsiooni põhiolekus. Proovifunktsioonina kasutame vesinikusarnase aatomi põhioleku 1s-lainefunktsiooni, milles tuumalaeng Z on asendatud efektiivse laenguga ![]() :
:
![]() .
.
(2.25)
Variatsiooniparameetriks ongi see laeng ![]() .
.
Jättes kõrvale lainefunktsiooni sõltuvuse spinnmuutujast, võib vastavalt Pauli printsiibile igal ruumiorbitalil olla kaks elektroni. Seega on He aatomi kaks elektroni ruumiliselt jaotuselt ning energeetiliselt identsetes olekutes. Süsteemi hamiltoniaan avaldub kujul:
![]() ,
,
(2.26)
kus
![]()
(2.27)
on ühe elektroni kineetilise energia operaator,
![]()
(2.28)
On elektroni ja He tuuma vahelise elektrostaatilise tõmbumise operaator ning
![]()
![]()
(2.29)
kahe elektroni elektrostaatilise tõukumise operaator.
Koguenergia keskväärtus koosneb siis võrrandi
![]()
(2.30)
vasakul poolel olevate vastavate integraalide keskväärtuste summast
![]() ,
,
(2.31)
kus
![]() ,
,
![]() (2.32)
(2.32)
![]()
(2.33)
ja
![]() .
.
(2.34)
Seega on energia keskväärtus
![]()
![]()
![]()
(2.35)
funktsioon efektiivsest tuumalaengust Z'.
Vastavalt variatsiooniprintsiibile leiame nüüd tingimusest
![]()
(2.36)
energia miinimumile vastava ![]() väärtuse. Kuna tingimuse (2.36) rakendamisel võrrandile (2.35) saame, et
väärtuse. Kuna tingimuse (2.36) rakendamisel võrrandile (2.35) saame, et
![]() ,
,
siis lõplikult on
![]() .
.
(2.37)
Seega on variatsioonimeetodil tehtud He aatomi elektronide orbitalid analoogilised vesinikusarnase aatomi orbitalidega. Üksnes reaalse tuumalaengu Z asemel tuleb kasutada efektiivset tuumalaengut Z'. Järelikult on elektronide omavahelisest interaktsioonist tingitud energia muutus aatomis taandatav tuuma positiivse laengu ekraneerimiseks ühe elektroni poolt teisele.
Elektroni energia He aatomis on siis vastavalt vesinikusarnase aatomi energia avaldisele (2.13):
![]() ,
,
(2.38)
kus C on nn. varjestuskonstant. Viimase valemi üldistus paljuelektroonsete aatomite mistahes elektroni energiatele empiiriliste varjestuskonstantidega C kannab Moseley' valemi nime.
§ 5. Kogu nurgamoment aatomis
Eespool vaatlesime He aatomi ülesandes ainult ruumilisi orbitale. Elektronide spinnist ja orbitaalsest pöörlemisest tingitud magnetmomentide vastasmõju leidmisel on oluliseks probleemiks kahe elektroni orbitaalse momendi ![]() ning spinnmomendi liitumine. Klassikalises füüsikas on kahe momendi liitmise järjekord suvaline. Kvanmehaanikas see pole aga nii. Vastavalt momentide vektormudelile võib nende liitmine toimuda siin vaid selliste nurkade all, mille korral resultantmoment oleks täisarvuline või 1/2-kordne.
ning spinnmomendi liitumine. Klassikalises füüsikas on kahe momendi liitmise järjekord suvaline. Kvanmehaanikas see pole aga nii. Vastavalt momentide vektormudelile võib nende liitmine toimuda siin vaid selliste nurkade all, mille korral resultantmoment oleks täisarvuline või 1/2-kordne.
Seetõttu võib kahe elektroni nelja momendi summeerimine He aatomis toimuda kahel viisil:
1. Liidame eraldi orbitaal- ja spinnmomendid (tulemuseks peavad olema täisarvud):
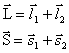
kusjuures kogumoment
![]()
(2.39)
on samuti avalduv täisarvuna. Selline liitmise reegel kannab LS-sideme e. Russell-Saundersi sideme nime. LS-side vastab momendi jäävuse kehtivuse seadusele eraldi orbitaal- ja spinnmomentidele.
2. Iga elektroni jaoks võib summeerida kõigepealt tema orbitaal- ja spinnmomendi:
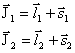
ning kogumoment aatomis on leitav üksikute elektronide momentide täisarvulise vektorsummana:
![]() .
.
(2.40)
Taoline liitmise reegel kannab (jj)-sideme nime.
Üldjuhul võib erinevalt saadud kogumoment aatomis olle erinev, s.t.
![]() .
.
(2.41)
Ühte või teist tüüpi sideme olemasolu aatomis on ära määratud kahe elektroni elektrostaatilise vastasmõju ning spinnorbitaalse vastasmõju energia suhtega. Viimane on proportsionaalne tuumalaengu neljanda astmega
![]()
(2.42)
(vesinikusarnases aatomis). Eespool nägime, et elektronide elektrostaatiline vastasmõju ![]() on aga vaid proportsionaalne efektiivse tuumalaenguga (vt. (2.34)). Seega on nende kahe mõju omavahelise suhte suurus oluliselt sõltuv efektiivsest tuumalangust. Kergemate elementide korral on see väike ning
on aga vaid proportsionaalne efektiivse tuumalaenguga (vt. (2.34)). Seega on nende kahe mõju omavahelise suhte suurus oluliselt sõltuv efektiivsest tuumalangust. Kergemate elementide korral on see väike ning
![]() .
.
(2.43)
Sellisel juhul realiseerub LS-side. Raskemate elementide korral on efektiivne tuumalaeng sisekihtide elektronidele suur ning vastavalt
![]() .
.
(2.44)
Nende aatomite kogumomendi leidmisel tuleb kasutada (jj)-sideme reeglit.
§ 6. Paljuelektroonsete aatomite termide klassifikatsioon
Mitut elektroni sisaldavate energianivoode põhistruktuur on ära määratud elektronide kineetilise energia ning nende tuumadega tõmbumise ning vastastikuse tõukumise potentsiaalse energiaga. Lisaks sellele eksisteerib aga veel magnetmomentide interaktsioonist tingitud energeetiline peenstruktuur aatomis.
Aatomi summaarne energeetiline olek kannab termi nime. Vaatleme järgnevalt termide klassifikatsiooni ning tähistust. Alustame aatomitest, mida iseloomustab LS-side. Nende korral on elektronide orbitaalne ja spinnliikumise vaadeldavad sõltumatutena ning aatomi kogu orbitaalne moment
![]()
(2.45)
on määratud kogu orbitaalse kvantarvuga L. Viimane on leitav lõplikult mittetäidetud elektronkihtide elektronide orbitaalsete kvantarvude l vektorsummana. Nii näiteks on Na aatomi summaarse orbitaalse momendi eest vastutav vaid tema 3s elektron, sisekihtide elektronide momendid on aga paarikaupa kompenseeritud.
Sõltuvalt kvantarvu L väärtusest tähistatakse aatomite terme järgmiselt:
L 0 1 2 3 4
sümbol S P D F G
Tegemist on samasuguste sümbolitega nagu erinevatele orbitaalsetele kvantarvule l vastavatel orbitalidel, siin on üksnes kasutatud suuri tähti.
Joonisel 7 on toodud vektormomentide liitmise näited L arvutamiseks elektronkonfiguratsioonide ![]() korral. (Meenutame, et vektorite kvantsummeerimisel on lubatud vaid täisarvulised resultantvektorite väärtused).
korral. (Meenutame, et vektorite kvantsummeerimisel on lubatud vaid täisarvulised resultantvektorite väärtused).
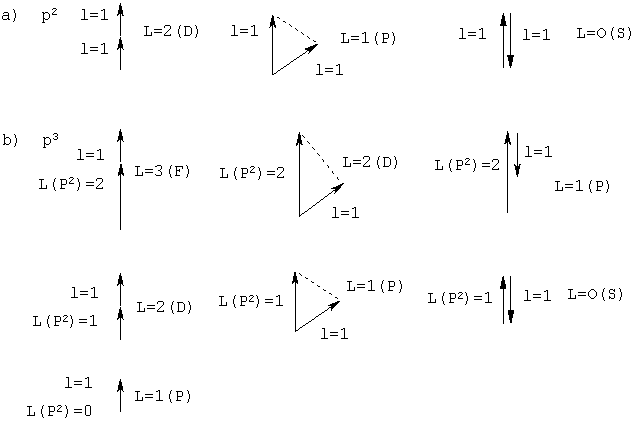
Joonis 7. Elektronide orbitaalse nurgamomendi liitmine p2- ja p3-süsteemis
Spinnide liitmine summaarse spinnmomendi leidmiseks Russell'i-Saunders'i sidemega aatomitel toimub analoogiliselt orbitaalsete nurgamomentide liitmisega. Silmas tuleb pidada siin seda, et elektroni spinnile vastava kvantarvu väärtus võib olla ![]() . Kahe elektroni süsteemis on summaarse spinni S väärtused järgmiste võimalike väärtusetega:
. Kahe elektroni süsteemis on summaarse spinni S väärtused järgmiste võimalike väärtusetega:
S = 1 (paralleelsed spinnid),
S = 0 (antiparalleelsed spinnid).
Termi spinnkvantarvu S iseloomustab tema multipleetsus. Multipleetsuse all mõistetakse termile vastava kogukvantarvu J erinevate võimalike väätuste arvu. Juhul kui ![]() , siis multipleetsus
, siis multipleetsus
![]() .
.
(2.46)
tingimusel ![]() on
on
![]() .
.
(2.47)
Termi sümbolis (vt. joonis 8) märgitakse multipleetsus vasakule üles.
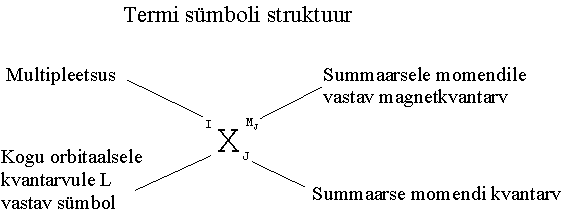
Joonis 8.
Tugeva spinnorbitaalse vastasmõjuga ((jj)-sidemega) aatomites iseloomustab pöördliikumist kogunurgamoment
![]() ,
,
(2.48)
kus J on kogunurgamomendi kvantarv. Viimane võib omada väärtusi:
![]() .
.
(Klebschi-Gordoni rida)
(2.49)
Joonisel 9 on toodud näide kogunurgamomendi kvantarvu J leidmiseks kahe mitteekvivalentse p-elektroni süsteemis.
Tabel 5
Elektronide kvantarvud
_________________________________________________________________
LS-side (jj)-side
_________________________________________________________________
|
peakvantarv n = 1, 2, 3, ... orbitaalne kvantarv
magnetkvantarv
spinnkvantarv |
peakvantarv n = 1, 2, 3, ... orbitaalne kvantarv
sisemine kvantarv
elektroni kogu liikumishulga
z-projektsioonile vastav kvantarv |
§ 7. Täitmise printsiip (aufbau) ja perioodilisuse süsteem
Mitut elektroni sisaldavates aatomites on elektronid paigutatud energeetilistele nivoodele vastavalt täitmise e. aufbau-printsiibile.Vastavalt sellele asub elektron kõige madalama energiaga olekus, kui see ei räägi vastu Pauli printsiibile.
Vesiniku aatomi põhiolekus on üks elektron, mis vastavalt aufbau-printsiibile asub 1s-nivool. He aatomis on kaks elektroni. Ei ole kahtlust, et esimene elektron paigutub siin s-orbitalile. Teise elektroni asetamine sellele orbitalile tõstab viimase energiat elektronide omavahelise tõukumise tõttu, kuid vaatamata sellele on 1s-nivoo ikkagi energeetiliselt madalaim ning He aatomi elektronstruktuur on 1s
2. Järgmiseks elemendiks perioodilisuse süsteemis on Li, mille aatom põhiolekus omab 3 elektroni. Esimesed kaks elektroni asuvad siin 1s-orbitalil. Mõnevõrra keerukam on aga kolmanda elektroni paigutamine. Vastavalt Pauli printsiibile peab ta olema järgmises, s.o. 2. elektronkihis. Lähtudes vesinikusarnase aatomi elektronide energiavoode avaldisest (2.13) sõltub nende väärtus üksnes peakvantarvust n. Seega on 2s- ja 2p-nivoo energeetiliselt ekvivalentsed. Millisele neist siis tuleks paigutada Li aatomi kolmas elektron? Nagu me nägime § II.4, võib elektronidevaheline elektrostaatiline vastasmõju olla vaadeldav ekraneerimise e. varjestusena. Vastavalt sellele on nii 2s- kui ka 2p-orbitalil asuva elektroni jaoks tuumalaeng varjestatud 1s-orbitalil oleva kahe elektroni poolt. See varjestus pole aga põhimõtteliselt ühesugune elektronile 2s- ja 2p-orbitalil. 2s-orbitali kujust järeldub, et elektroni leidmise tõenäosus tuumal on erinev nullist. Küll aga läbib tuuma nulltasand p-orbitalide korral. Järelikult on 2s-orbitalil asuva elektroni leidmise tõenäosus tuuma läheduses suurem võrreldes 2p-orbitalil oleva elektroniga (vt. joonis 10).
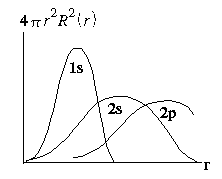
Joonis 10. Orbitalide radiaalne jaoutus Li aatomis
Järelikult on 2s-orbitalil olevad elektronid vähem varjestatud 1s-kihis olevate elektronide poolt ning nende tõmbumine tuumaga on suurem. Kuna vastav energianivoo on seetõttu madalamal, paigutub kolmas elektron Li aatomis 2s-orbitalile.
Järgnevatest elementidest on vastavuses ülaltoodud põhimõtetega Be aatom elektronkonfiguratsiooniga ![]() ja B aatom konfiguratsiooniga
ja B aatom konfiguratsiooniga ![]() . Problemaatiline on jällegi C aatomi elektronkonfiguratsioon, kus võib eristada järgmisi võimalikke elektronide paigutusi:
. Problemaatiline on jällegi C aatomi elektronkonfiguratsioon, kus võib eristada järgmisi võimalikke elektronide paigutusi:
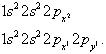
Eelistatud on teine konfiguratsioon ja seda kahel põhjusel:
1) erinevatel ruumiorbitalidel asuvad p-elektronid varjestavad üksteist vähem kui samal orbitalil olevad elektronid. Seetõttu paigutavad elektronid ekvivalentsete orbitalidele maksimaalselt eraldi asetatult (1. Hundi reegel);
2) üldjuhul väljendub Pauli printsiip keeluna kahele paralleelse spinniga elektronile samaaegselt ühes ja samas ruumipunktis viibimiseks. Seega on elektroni vahetus läheduses teise, paralleelse spinniga elektroni leidumise tõenäosus lähedane nullile, mis tingib nende elektronide vastastikuse elektrostaatilise tõukumise vähenemist. Seesugune nähtus on üldse iseloomulik fermionidele ning seetõttu kannab vastav ruumiosa elektroni ümber Fermi augu nime. Fermi augu olemasolust põhjustatud tõukumisenergia vähenemine (süsteemi stabiliseerumine) viib selleni, et erinevatel ekvivalentsetel ruumiorbitalidel asuvad elektronid püüavad olla paralleelsete spinnidega (2. Hundi reegel).
Vastavalt eeltoodud põhimõtetele on aufbau-printsiip kehtiv ka igas järgmise peakvantarvuga iseloomustatud elektronkihis, s.t. täitmise järjekord kihi piires on
3s 3p 3d
4s 4p 4d 4f jne.
Erinevusi täitmise järjekorras võib olla üleminekul ühest elektronkihist teise. Siin kehtib seaduspärasus, mille kohaselt täidetakse eelkõige orbitalid minimaalse kvantarvude summaga
![]()
(2.50)
Juhul kui summa ![]() on kahel orbitalil võrdne, täitub enne orbital suurema kõrvalkvantarvu l väärtusega. Üldine täitumise järjekord aatomi orbitalidel on toodud tabelis 6.
on kahel orbitalil võrdne, täitub enne orbital suurema kõrvalkvantarvu l väärtusega. Üldine täitumise järjekord aatomi orbitalidel on toodud tabelis 6.
Tabel 6
Aatomorbitalide täitumise järjekord
|
Orbital |
1s |
2s |
2p |
3s |
3p |
4s |
3d |
4p |
5s |
4d |
5p |
6s |
|
n + l |
1 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
5 |
6 |
6 |
6 |
|
l |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
Niisugune seaduspärasus põhjustab väga lähedaste keemiliste omadustega elementide (lantaniidid, aktiniidid) järjestikust paiknemist Mendelejevi perioodilisuse süsteemis. Keemiliste omaduste eest vastutavad eelkõige aatomi välimise e. valentskihi elektronid. Vastavalt elementidel jääda samaks (näit. 4s2) ning täidetakse sisekihi orbitale (näit. 3d).