Molekulide näol on tegemist kvantmehaaniliste süsteemidega, mis koosnevad mitmest elektronist ja aatomituumast. Vastavalt sellele on molekuli hamiltoniaan jagatav järgmisteks osadeks:

(3. 1)

kus on elektronide liikumisega seotud osa, - tuumade liikumisega seotud osa ning - elektronide ja tuumade vahelise vastasmõju hamiltoniaan.

N aatomituuma ja m elektroni sisaldava molekuli korral välises elektriväljas tugevusega ja magnetväljas tugevusega on üksikute panuste kuju hamiltoniaani järgmine.

Esiteks:

(3. 2)

kus on elektronide liikumisega seotud nurgamoment, -elektronide magnetmoment ja -välise elektrivälja potentsiaal. Nurksulgudes olevas avaldises arvestavad järjestikused liikmed elektronide kineetilist energiat, elektronide vastasmõju välise elektri- ja magnetväljaga ning elektronide spinnorbitaalset vastasmõju. Viimasena on kahekordse summana toodud elektronide elektrostaatilist tõukumist arvestav liige.

Teiseks:

(3. 3)

kus on vastavalt tuuma laeng ja mass, aga tema magnetmoment. Järjestikused liikmed avaldises (3.3) arvestatavad jällegi tuumade kineetilist energiat, vastasmõju välise elektri- ja magnetväljaga ning vastastikust elektrostaatilist tõukumist.

Kolmandaks:

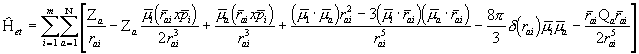(3. 4)

.

(3. 5)

Edaspidises käsitluses lähtumegi molekuli hamiltoniaanist viimati toodud kujul.

Enamikus kaasaegsetes kvantkeemilistes meetodites tehakse veel üks oluline molekuli hamiltoniaani lihtsustav lähendus (Born, Oppenheimer, 1927). Eeldatakse, et aatomituumade ja elektronide massi suure erinevuse tõttu (prootoni mass on ligikaudu 1836 korda suurem elektroni massist) võib elektronide liikumist molekulis vaadelda praktiliselt paigalseisvate tuumade väljas. Impulsi jäävuse seadusest võib välja arvutada, et elektroni suhtelisele nihkele 1 m võrra vastab tuumade nihe vaid veidi enam kui 0,5 mm. Kuivõrd aatomituumade ning elektronide liikumine on praktiliselt sõltumatu, võib molekuli kogulainefunktsiooni esitada sõltumatute elektronide lainefunktsiooni ja tuumade lainefunktsiooni korrutisena:

.

(3. 6)

Borni-Oppenheimeri lähenduses võib lugeda tuumade lainefunktsiooni konstantseks. Elektronide lainefunktsioon on leitav aga elektroonse Schrödingeri võrrandi

(3. 7)

lahendina, kus

(3. 8)

on elektronide hamiltoniaan ning elektronide energia. Molekuli koguenergia leidmisel tuleb arvestada ka lihtsalt Coulomb'i seadusest arvutatud tuumade tõukumise energiat:

.

(3. 9)

Võrrandi (3.7) lahendamisel saadav elektroonne energia on vaadeldav edasi potentsiaalse energiana tuumade liikumise jaoks. Seega vastab Borni-Oppenheimeri lähenduses igale tuumade konfiguratsioonile kindel molekuli koguenergia . Kaheaatomilise molekuli korral on viimane vaadeldav funktsioonina tuumade omavahelisest kaugusest (vt. joonis 11). Tulemusena saadakse keemilise sideme dissotsiatsioonikõver. Dissotsiatsioonikõvera väärtuste vahe lõpmatuses ning miinimumis annab sideme teoreetilise dissotsiatsioonienergia. Viimane erineb eksperimentaalsest molekuli võnkumisest ning pöörlemisest sidemete ümber tingitud nn. nullenergia võrra.

molekuli dissotsiatsioonikõver

Mitteaatomiliste molekulide korral iseloomustavad molekuli energia sõltuvust tuumade konfiguratsioonist mitmemõõtmelised energia pinnad ja hüperpinnad. Viimaste piltlikuks kujutamiseks kasutatakse mitmesuguseid ristlõikeid. Borni-Oppenheimeri lähendust kasutavate kvantkeemiliste meetodite täpsuse määramiseks on vaja hinnata selle lähendusega tehtavat viga. Suurima suhtelise veaga peaks olema kergemaid tuumi sisaldava molekuli energia. Vastavad arvutused näitavad, et molekuli dissotsiatsioonienergia põhiolekust on 0,16491478 , Borni-Oppenheimeri lähenduse rakendamisel aga 0,16488830 . See vastab dissotsiatsioonienergiate erinevusele 0,695 kJ/mol e. suhteliselt 0,016 % molekuli korral on suhteline erinevus juba 0,007 % ning see väheneb progresseeruvalt raskemaid aatomituumi sisaldavate ühendite jaoks. Järelikult võib keemilise täpsuse piires Borni-Oppenheimeri lähenduse lugeda lubatavaks.

Asjaolu, et elektronide ja tuumade liikumine on vaadeldavad sõltumatutena, hõlbustab oluliselt ka molekulide spektrite klassifitseerimist.

Vaatleme järgnevalt kahte teoreemi, mis võivad osutuda kasulikuks molekulide lainefunktsioonide ja keemilise sideme analüüsil.

Viriaali teoreem.

Olgu meil hamiltoniaaniga kirjeldatud molekul statsionaarses olekus, s.t. puudub energiavahetus keskkonnaga. Siis mistahes hermiitse operaatori jaoks kehtib hüperviriaali teoreem:

,

(3. 10)

mis sisuliselt tähendab seda, et nende operaatorite keskväärtused ei muutu ajas.

Olgu operaator A järgmise kujuga: (alates 63-64)

,

(3. 11)

kus summeerimine on teostatud üle kõigi osakeste koordinaatide . Siis

,

(3. 12)

kus ja on vastavalt süsteemi kogu potentsiaalse ja kineetilise energia operaatorid.

Lähtudes hüperviriaali teoreemist (3.10), saame

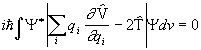
(3. 13a)

ehk

.

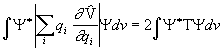(3.13b)

Leides integraalidele vastavad keskväärtused, saame

.

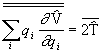(3. 14)

Viimane valem ongi kvantmehaaniliseks viriaali teoreemiks. Kasutades potentsiaali operaatorit konkreetsel kujul, võib viriaali teoreemi veelgi lihtsustada. Olgu homogeenne n astme funktsioon Cartesiuse koordinaatidest. Siis

(3. 15)

ja järelikult

.

(3. 16)

Kuna süsteemi koguenergia

,

(3. 17)

siis on kehtivad järgmised seosed süsteemi kineetilise, potentsiaalse ja koguenergia vahel:

,

(3. 18a)

.

(3.18b)

Erijuhul, kui on tegemist elektrostaatilise vastasmõjuga potentsiaalses energias (n = -1), võib viriaali teoreemi väljendada kujul:

(3. 19a)

ehk

(3.19b)

ehk

.

(3.19c)

Süsteemi, mille potentsiaalne energia on koordinaatide homogeenne funktsioon, tõeline lainefunktsioon peab rahuldama viriaali teoreemi. Tuues variatsiooniparameetrina sisse kordaja iga ristkoordinaadi ees, ning minimeerides variatsiooniliselt viriaali teoreemi rahuldavat lainefunktsiooni. Selline protseduur kannab skaleerimise nime. Kooskõlalise välja meetodil leitud lainefunktsioonid peavad rahuldama viriaali teoreemi ning seetõttu kasutatakse arvutatud kineetilise ja potentsiaalse energia suhet olulise kriteeriumina lainefunktsiooni headuse hindamisel.

Hellmanni-Feynmani teoreem.

Hellmanni-Feynmani teoreem väidab, et energia gradient mingi parameetri suhtes on võrdne hamiltoniaani gradiendi keskväärtusega sama parameetri suhtes, s.t.

.

(3. 20)

Parameeter (näiteks tuuma koordinaat) peab loomulikult sisalduma hamiltoniaani avaldises . Hellmanni-Feynmani teoreem võimaldab oluliselt lihtsustada molekulide mitmesuguste omaduste arvutamist - selle asemel, et leida energia tuletist antud parameetri suhtes, piisab vaid hamiltoniaani diferentseerimisest ning vastava keskväärtuse (3.20) leidmisest. Tuleb rõhutada aga, et Hellmanni-Feynmani teoreemi rahuldavad lainefunktsioonid peavad olema täpsed. Isegi väikesed kõrvalekaldumised tõelisest lainefunktsioonist võivad põhjustada suuri vigu omaduste arvutamisel. Seega võib Hellmanni-Feynmani teoreemi abil arvutatud molekulide omaduste (elektriline ja magnetiline läbitavus, tasakaaluline geomeetria jms.) võrdlust eksperimentaalsete väärtustega kasutada samuti arvutatud molekuli lainefunktsiooni kvaliteedi hindamiseks.

Hellmann ja Feynman kasutasid teoreemi (3.20) sõltumatult teineteisest juhtumi jaoks, kus esitab tuumade ristkoordinaate. Järeldusena leidsid nad, et Borni-Oppenheimeri lähenduse kasutamise korral võib mistahes aatomi tuumale mõjuva jõu molekulis arvutada vastavalt klassikalisele elektrostaatikale eeldusel, et on teada täpne kvantmehaaniline elektronide jaotus (elektrostaatiline Hellmanni-Feynmani teoreem). Seega annab tasakaalulise geomeetriaga molekulide korral viimane järeldus võimaluse leida molekulide sidemeenergiaid, lähtudes lihtsatest klassikalistest elektrostaatilistest mudelitest.

Sõltuvalt proovifunktsiooni valikust variatsioonimeetodil või häirimata süsteemi lainefunktsioonist häiritusmeetodil võib molekuli lainefunktsiooni matemaatiline kuju olla küllaltki erinev. Praktikas on enam kasutust leidnud järgmised molekulide elektroonsed lainefunktsioonid, millest tulenevad vastavate kvantkeemiliste meetodite nimetused.

a) Valentssidemete (VB-) meetod.

Molekuli lainefunktsioon leitakse lineaarkombinatsioonina Slateri determinantidest :

,

(3. 21)

kus Ai on variatsioonikordaja ning determinandis

(3. 22)

kasutatakse elektronide lainefunktsioonidena naaberaatomite valentskihi elektronide aatomorbitale .

b) Molekulaarorbitalide (LCAO MO) meetod .

Molekuli lainefunktsioon on antud ühe determinandina

,

(3. 23)

mis harilikult vastab molekuli põhioleku elektronkonfiguratsioonile. Üheelketroonsete lainefunktsioonidena kasutatakse determinandis

(3. 24)

molekulaarorbitale (MO):

,

(3. 25)

c) Konfiguratsioonilise interaktsiooni (CI) meetod .

Molekuli lainefunktsioon leitakse lineaarkombinatsioonina Slateri determinantidest :

,

(3. 26)

kus determinandid

(3. 27)

koosnevad MO-dest. Viimased on enamasti leitud LCAO MO meetodil molekuli põhioleku jaoks, kuid erinevad determinandid vastavad molekuli erinevatele elektronkonfiguratsioonidele (põhiolek, ühe- ja kahekordselt ergastatud olekud jne.). Mõningad elektronkonfiguratsioonid LiH molekuli jaoks on toodud joonisel 12.

LiH molekuli põhiolek (a), ühekordselt ergastatud olek (b) ning kahekordselt ergastatud olek (c).

Täieliku (lõpmatu) baasi kasutamisel peavad VB- ja CI-meetod andma sama tulemuse. Reaalsetes arvutustes kasutatakse mittetäielikku baasi ning seetõttu on neil meetoditel saadud tulemused mõnevõrra erinevad. Eelistatud on CI-meetodil saadud tulemused, kuna konfiguratsioonilises interaktsioonis leiavad arvestamist ka keemilist sidet mittemoodustavad elektronid.

d) multikonfiguratsiooniline kooskõlalise välja (MC SCF) meetod.

Molekuli lainefunktsioon on moodustatud taas determinantidest

,

(3. 28)

mis omakorda koosnevad molekulaarorbitalidest

.

(3.25)

Erinevalt CI-meetodist, kus variatsiooniliselt leitakse vaid determinantide ees olevad kordajad Di (vt. 3.26), on MC SCF meetodis variatsioonikordajateks nii Bi kui ka MO koefitsiendid cik . Meetod on seetõttu olemasolevatest kõige täpsem, kuid ühtlasi ka kõige töömahukam. Seetõttu on ta rakendust leidnud vaid väikese arvu elektronidega molekulide korral.

e) Hajunud lainete (SW- e. MS-) meetod.

Molekuli vaadeldakse koosnevana kolme tüüpi piirkonnast, milles elektronile mõjuva potentsiaali kuju on erinev (vt. joon. 13.). Iga aatomituuma ümber on kujuteldav sfääriline pind (muffin-tin e. MT-sfäär), milles keskmine elektrostaatiline potentsiaal vastab Kepleri ülesandest tuntud tsentraalvälja potentsiaalile.

Molekuli AB jaotus SW-meetodis.

Üheelektroonsed lainefunktsioonid on selles piirkonnas antud lineaarkombinatsioonidena AO-dest:

(3. 29)

MT -sfäärid omavahel ei kattu.

Sfääride vahel asub piirkond II, milles elektronidele mõjub konstantse väärtusega potentsiaal. Lugedes selle potentsiaali suvaliselt võrdseks nulliga, saame elektronide lainefunktsioonideks selles piirkonnas vaba elektroni Schrödingeri võrrandi

(3. 30)

lahendid:

,

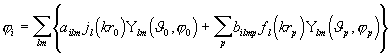(3. 31)

kus on sfäärilised harmoonikud ning ja vastavalt Besseli sfäärilised funktsioonid ning Hankeli funktsioonid. Lahendeid (3.31) nimetatakse ka tasalaineteks.

Piirkonnas III, mis asub väljaspool kogu molekuli ümbritsevat suurt sfääri, mõjub jällegi tsentraalsümmeetriline potentsiaal, kuid nüüd juba selle sfääri keskpunkti suhtes. Lainefunktsioonid

(3. 32)

on esitatavad sellele tsentraalväljale vastavate lainefunktsioonide lineaarkombinatsioonina. Koefitsiendid leitakse mitte variatsiooniliselt, vaid funktsioonide tingimustest sfääride pinnal.

Hajunud lainete meetod on eriti palju rakendust leidnud kristallide kvantmehaanikas.

f) Ujuvate orbitalide (FSGO) meetod.

Molekuli lainefunktsioon esitatakse ühe determinandina

(3. 33)

orbitalidest , mis on üldjuhul tsentreeritud mitte aatomituumadele, vaid mingitesse teistesse ruumipunktidesse molekuli piires. Orbitalidena kasutatakse enamasti sfäärilisi Gaussi funktsioone:

,

(3. 34)

kus varieeritavateks parameetriteks on eksponendikordaja ning orbitali tsentri asukohavektor ( on elektroni raadiusvektor molekuli koordinaatteljestiku suhtes). Ujuvate orbitalidena saadud lainefunktsioone iseloomustab suur paindlikus, kuna nad võivad muuta oma lokalisatsiooni ulatust (kokku tõmbuda või laieneda) sõltuvalt parameetrist ning samuti asukohta molekulis (). Meetodi positiivseks küljeks on ka see, et kasutades sfäärilisi Gaussi funktsioone, osutuvad molekuli energia integraalid väga lihtsalt leitavateks. Seetõttu on FSGO meetod laialdast rakendust leidnud suurte (bio)molekulide kvantkeemilisel arvutusel.

Ajalooliselt esimeseks molekulide Schrödingeri võrrandi lahendamise kvantmehaaniliseks meetodiks on H. Heitleri ja F. Londoni esitatud (1927) valentssidemete meetod.

Vaatleme kahte vesiniku aatomit, Ha ja Hb, mis asuvad üksteisest lõpmatult kaugel. Igasugune vastasmõju kahe aatomi osakeste vahel on siis välistatud ning kummagi aatomis oleva elektroni lainefunktsioonid on vaadeldavad mittehäiritud H-sarnaste orbitalidena. Tähistame põhioleku 1s-funktsioonid kummalgi aatomil vastavalt , kus sulgudes on antud elektroni indeks. Elektronide liikumise sõltumatuse tõttu on süsteemi lainefunktsioon

(3. 35)

avalduv lihtsa korrutisena AO-dest.

Süsteemi kogu hamiltoniaan

(3. 36)

ning isoleeritud aatomite Schrödingeri võrrandi lahendustest tuleneb, et

,

(3. 37)

s.t. süsteemi koguenergia on isoleeritud aatomite energiate summas.

Lahendame nüüd need kaks H aatomit molekulis reaalsele sidemepikkusele vastavale kaugusele teineteisest. Seejuures tekib potentsiaalses energias kolme uue vastasmõju arvestamise vajadus:

a) elektronide elektrostaatiline tõukumine;

b) tuumade elektrostaatiline tõukumine;

c) ühe aatomi elektroni tõmbumine teise aatomi tuumaga.

Vastavalt muutunud süsteemi hamiltoniaan on kujul:

,

(3. 38)

kus

.

(3. 39)

Viimases avaldises olevate raadiuste sisu on toodud joonisel 14.

molekuli ülesanne.

Kahe H aatomi lähendamisel muutub ka süsteemi lainefunktsioon, kuna mitme elektroni süsteemina peab ta rahuldama antisümmeetria tingimust.

Ruumiliste orbitalide ja spinnlainefunktsioonide sõltumatuse tõttu saab kogulainefunktsiooni välja kirjutada kahe erineva Slateri determinandina:

,

(3. 40a)

,

(3.40b)

kus ja on lainefunktsiooni ruumilise osa normeerimiskordajad, aga spinnosa normeerimiskordaja. Esimene lainefunktsioon on sümmeetriline e. paarisfunktsioon elektronide vastastikuse ümberpaigutuse suhtes ruumiorbitalidel, mistõttu teda tähistatakse ka indeksiga g (sks. k. gerade).

Lainefunktsioon on aga antisümmeetriline e. paaritu elektronide ruumikoordinaatide vahetuse suhtes (sks. k. ungerade).

Leiame molekuli elektroonse energia mõlema lainefunktsiooni korral. Vastavalt keskväärtusteoreemile on elektroonne energia lainefunktsioon korral :

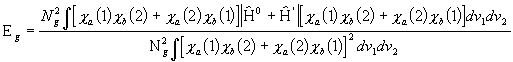
(3. 41a)

ning lainefunktsiooni korral:

.

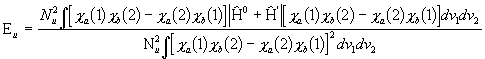(3.41b)

Viime sisse järgmised integraalide tähistused. Integraal

(3. 42)

on lihtsalt H aatomi energia isoleeritud olekus.

Kuloniline integraal

(3. 43)

väljendab esimese ja teise elektroni tõukumist, tuumade tõukumist ning elektronide tõmbumist teise aatomi tuumaga.

Vahetusintegraal

(3. 44)

kujutab endast kahe tuuma ja kahe elektroni süsteemi elektrostaatilist energiat, kui elektronide tõenäosuse tihedus on väljendatud AO-de segakorrutisena . Joonisel 15. on toodud kulonililse ja vahetusintegraali sõltuvus tuumadevahelisest kaugusest -s.

molekuli energia ja molekulaarintegraalide sõltuvus tuumadevahelisest kaugusest.

Kattumisintegraal

(3. 45)

erineb nullist, kuna erinevatesse ruumipunktidesse tsentreeritud AO-d pole enam ortogonaalsed.

Teostades vastavad asendused elektroonse energia avaldistesse (3.41), saame

(3. 46a)

ja

.

(3.46b)

Ülaltoodud lihtsal Heitleri ja Londoni esitatud VB-meetodil saadud molekuli sidemeenergia erineb eksperimentaalsest umbes 34 % ning tasakaaluline sidemepikkus 15 % (vt. tabel 7.). See on muidugi mitterahuldav keemias vajamineva täpsuse jaoks.

Seetõttu käsitleme järgnevalt mõningaid tuntumaid võtteid VB-meetodi parandamiseks.

(3. 47)

sidemepikkuse lühenemise korral. Tõepoolest, piirjuhul on tegemist tuumaga, mille efektiivne tuumalaeng 1,625 kahe elektroni süsteemi jaoks. Joonisel 16. on näidatud efektiivse tuumalaengu sõltuvus vesiniku 1s-orbitalidel sõltuvalt tuumadevahelisest kaugusest. Tasakaalulise sidemepikkuse korral on variatsiooniparameetrina leitud 1,166. Parandatud lainefunktsioonide (3.47) kasutamine VB meetodis annab oluliselt parema sidemeenergia ning praktiliselt õige sidemepikkuse väärtuse (vt. tabel 7.).

Tabel 7

molekuli energia VB-meetodil mitmesugustes lähendustes.

2) Järgmise täienduse VB-meetodile saab teha, lähtudes alljärgnevast füüsikalisest kaalutlusest. On ilmne, et aatomite lähenemisel üksteisele kaotab elektronidele mõjuv potentsiaal sfäärilise sümmeetria. Toimub aatomite elektronkatete polariseerumine, s.t. ka nende laengujaotus pole enam sfäärsümmeetriline. Kuna polariseeriv mõju toimib eelkõige piki tuumi ühendavat sirget (keemilist sidet), siis võib seda efekti arvestada molekuli lainefunktsioonis kõrgema kõrvalkvantarvuga orbitalide e. polarisatsiooni-funktsioonide lisamisega. Lugedes süsteemis x-teljeks sideme suuna, oleks sellisteks polarisatsioonifunktsioonideks -AO-d. Vastavalt sellele tuleks ühel aatomil lokaliseeritud aatomifunktsioonid kujutada järgmiselt:

,

(3. 48)

kus N on normeerimiskordaja, aga variatsioonikordajad, mis määratakse koguenergia miinimumi tingimusest. Polarisatsioonifunktsioonide kasutamine parandab veelgi VB-meetodil saadud lahendite kvaliteeti (vt. tabel 7).

3) Molekuli lainefunktsiooni parandamiseks VB-meetodis võib kasutada ka järgmist klassikalisel keemilisel struktuutiteoorial põhinevat ideed. On loogiline, et aatomite lähenemisel teineteisele süsteemis suureneb selliste olekute tõenäosus, kus antud ajahetkel on kaks elektroni ühe tuuma ligiduses. Taoline hetkeline struktuur vastaks siis zwitterioonsetele vormidele . Juhul, kui mõlemad elektronid on tuuma juures, avaldub süsteemi lainefunktsioon kujul

,

kus lainefunktsioonis

(3. 49)

on efektiivne tuumalaeng . Mõlema H tuuma identsuse tõttu vastab molekuli ioonsetele piirstruktuuridele sümmeetriline lainefunktsioon:

.

(3. 50)

Molekuli kogulainefunktsiooni võib leida aga järgmiselt:

,

(3. 51)

kus arvutatakse mingil eespool toodud lähenduse tasemel, aga järjekordseks variatsiooniparameetriks, mille optimeerimine parandab veelgi süsteemi sidemeenergia väärtust (vt. tabel 7.)

4) Vastavalt antisümmeetria printsiibile ei saa kaks paralleelse spinniga elektroni asuda samaaegselt samas ruumipunktis. Elektronide omavahelise elektrostaatilise tõukumise tõttu kehtib samasugune keeld aga mistahes kahe elektroni jaoks sõltumatult nende spinni väärtusest. Eespool toodud lainefunktsioonid ei arvesta aga sellist piirangut. Seetõttu on vastav elektronide tõukumise destabiliseeriv energia ülehinnatud ning saadud sidemeenergiad liiga madalad (vt. tabel 7) H. M. James ja A.S. Coolidge (1933) soovitasid sellise vea parandamiseks molekuli lainefunktsiooni läbi korrutada mingi parandusfunktsiooniga , mis sisaldab ilmutatud kujul elektronide omavahelist kaugust . Seejuures

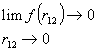
ning seega ka

(nullilise tõenäosusega olek).

Funktsioon võib olla esitatud matemaatilise reana, mis sisaldab mitmeid variatsiooniparameetreid. W. Kotos on arvutanud James-Coolidge'i meetodil molekuli sidemeenergia eksperimentaalse täpsuse piires, kasutades rittaarenduses 50 liiget (vt. tabel 7). Suuremate molekulide korral muutub James'i Coolidge'i lainefunktsioon aga erakordselt keerukaks ning seetõttu pole selliselt parandatud VB-meetod praktilist rakendust leidnud.

determinanti. Järelikult kasvab paralleelselt aatomite arvuga süsteemis kiiresti vajalike arvutuste maht, mis piirab samuti VB-meetodi rakendamist suuremate molekulide korral.

Kuigi VB-meetod ei ole praktilistes arvutustes eriti levinud, seostub temaga siiski mitme kvantkeemilise mudeli sissetoomine keemiliste ühendite struktuuriteooriasse. Järgnevalt puudutame neist lähemalt valentsolu ja hübridisatsiooni mõistet.

.

(3. 52)

.

(3. 53)

.

(3. 54)

Molekulaarspektrites hübriidorbitalide vastavaid üleminekuid jälgida ei ole võimalik, kuna tegemist on lihtsalt VB-meetodile kohandatud matemaatiliste konstruktsioonidega, mitte aga reaalsete üheelektroonsete orbitalidega.

Teise perioodi elementide aatomite valentskihi orbitalidest võib moodustada kolme tüüpi hübriidorbitale:

a) -hübriidorbitalid on saadud 2s- ja ühe 2p-orbitali lineaarkombinatsioonina:

.

(3. 55)

Igal sp-olekus aatomil on kaks hübriidset sp-orbitali ning 2 häirimata p-orbitali valentskihis. Hübriidorbitali kuju on toodud joonisel 17.

b) -hübriidorbitalid moodustatakse kahest 2p-orbitalist ning ühest 2s-orbitalist:

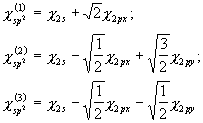
(3. 56)

-hübriidorbitale on antud aatomil 3 ning nende kuju on lähedane sp-hübriidorbitali kujuga. Kolm orbitali asuvad aga ühes tasandis ning nurk nende telgede vahel on 120º (vt. joonis 17).

Hübriidorbitalide kuju

c) -hübriidorbitalid koosnevad 2s-orbitalist, mis on kombineeritud kõigi 3 2p-orbitaliga.

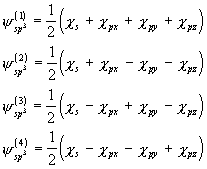
(3. 57)

Neli -hübriidorbitali on ruumiliselt suunatud korrapärase tetraeedri nurkadesse, kujult on nad aga sarnased sp-hübriidorbitalidega (vt. joonis 17).

Hübriidorbitale võib moodustada ka kõrgema peakvantarvuga ja kõrvalkvantarvuga orbitalidest (vt. tabel 8).

Kuigi hübridisatsiooni mõiste on osutunud väga viljakaks paljude orgaaniliste ühendite struktuuri kvalitatiivsel kirjeldamisel, ei oma ta erilist tähtsust kõige levinumas kvantkeemilises meetodis - MO-meetodis.

Järgnevalt siirdumegi MO-meetodiga seonduvate probleemide juurde.

Tabel 8

Molekuli elektronide kogulainefunktsioon avaldatakse LCAO MO meetodis ühe determinandina

,

(3. 58)

kus üheelektroonseteks lainefunktsioonideks on molekulaarorbitalid (MO-d) lineaarkombinatsioonidena aatomorbitalidest (AO-dest):

.

(3. 59)

Keskseks probleemiks on selles rittaarenduses baasifunktsioonide valik.

Praktilistes arvutustes võib baasina kasutada mitmesuguse matemaatilise kujuga funktsioone. Teoreetiliselt on täpsete MO-de saamiseks vaja kasutada mingit täielikku baasi, mis aga enamasti koosneb lõpmatust hulgast baasifunktsioonidest ning võib veel sisaldada pidevale energeetilisele spektrile vastavat lainefunktsiooni osa:

,

(3. 60)

kus on spektraalsagedus. Praktikas tuleb aga arvutusteks kuluva aja ja arvutimälu lõplikkuse tõttu piirduda suhteliselt väikese hulga baasifunktsioonidega.

Üldjuhul on LCAO MO meetodis vajalike üheelektroonsete integraalide arv

(3. 61a)

ja kaheelektroonsete integraalide arv

(3.61b)

kiiresti kasvav baasifunktsioonide arvu N suurenedes. Seetõttu kasutatakse paljudel juhtudel baasi, kus iga aatomi jaoks molekulis kasutatakse vaid selliseid AO-sid, mis vastavad selle aatomi osaliselt või täielikult täidetud elektronkihtidele aatomi põhiolekus. Nii on selliseks baasiks järgmised AO-d:

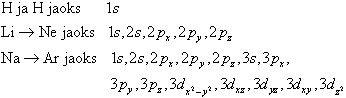
Taolist baasi nimetatakse minimaalseks baasiks. Arvutustes kasutatavaid baase tähistatakse tihti vastavate baasi AO-de tähistega ümarsulgudes. Minimaalseks baasiks I perioodi elementidele on (1s), II perioodi elementidele (2s, 1p) ning III perioodi elementidele (3s, 2p, 1d). Arv orbitali tüüpi märkiva tähe ees näitab antud tüüpi orbitalide erinevate komplektide arvu.

Baasifunktsioonide arvu suurendamine võib märgatavalt parandada arvutustulemusi. Olulist efekti annab iga minimaalses baasis kasutatava AO kujutamine kahe sama tüüpi, kuid erineva eksponendinäitajaga AO lineaarkombinatsioonina:

.

(3. 62)

Sellist baasi nimetatakse topelt-dzeeta (DZ) baasiks. Üldjuhul nimetatakse baase, kus igale AO-le vastab rohkem kui üks elementaarne baasifunktsioon, laiendatud baasideks.

Nii nagu VB- meetodis, võib ka MO-meetodis lainefunktsiooni kvaliteedi parandamiseks kasutada baasis antud aatomi jaoks mittetäidetud elektronkihtidele vastavaid suurema kõrvalkvantarvuga (l) orbitale ehk polarisatsioonifunktsioone (p). I perioodi elementide jaoks on polarisatsioonifunktsioonideks 2p, 3d jne., II perioodi jaoks 3d, 4f jne.

Baasi laiendamisel on oluline teada, et isegi funktsioonide arvu piiramatu kasvu korral ei ole võimalik saada ka piirjuhul molekuli tõelise energia väärtust LCAO MO meetodiga. Molekuli lainefunktsioon esitatakse siin ühe determinandina (IPM lähendus), mistõttu baasi laiendamisel koondub energia mingile teisele kindlale (kõrgemale) väärtusele. Seda energia väärtust antud molekuli jaoks nimetatakse Hartree-Focki piiriks (HFL).

Jooniselt 18 ilmneb molekuli näitel, et HFL lähedasi tulemusi võib saada juba küllalt piiratud baasi korral. Oluline on silmas pidada järgmisi reegleid:

molekuli arvutusliku energia sõltuvus baasi suurusest.

1) suurima paranduse energiasse toob kaasa üleminek minimaalselt baasilt DZ-täpsusega baasile;

2) edasine baasifunktsioonide arvu suurendamine aatomite valentskihis on väga väikese efektiga;

3) järgmise suurema paranduse energiasse annab ühe polarisatsioonifunktsiooni sissetoomine igale aatomile (DZ + P baas). Viimase kasutamisel saab juba väga lähedase tulemuse HFL-le.

Edasine polarisatsioonifunktsioonide lisamine baasile praktilist efekti ei anna.

Baasi valikul LCAO MO meetodis tuleb veel silmas pidada, et tegemist oleks tasakaalustatud baasiga, s.t. erinevat tüüpi baasifunktsioonide arvu suhe peab vastama kindlale suurusele. Nii on soovitatud II perioodi elementide korral kasutada tasakaalulise baasina baasifunktsioonide komplekte, kus s- ja p-tüüpi funktsioonide suhe oleks 3/1, 4/2, 5/3, 7/4 jne. Mittetasakaalustatud baasi kasutamine võib viia absurdsetele tulemustele molekuli laengujaotuse kohta.

Tabelis 9 on toodud nõuded baasi kvaliteedi kohta molekulide mitmesuguste füüsikaliste ja keemiliste omaduste leidmisel LCAO MO meetodil.

Tabel 9

Baasi valiku reeglid LCAO MO meetodis

Üldkujul avalduvad baasifunktsioonid järgmiselt:

,

(3. 63)

kus on funktsiooni radiaalne osa ning antud funktsiooni tüübile vastav sfääriline harmoonik. Baasi tüüp on antud just kasutatud radiaalse osa kujuga.

1. Vesinikusarnased orbitalid.

Keemia loogikast lähtudes võiks antud elemendi aatomile kõige paremaks baasiks olla vesinikusarnased orbitalid (vt. II ptk., §2), mille radiaalosa on

,

(3. 64)

kus n ja l on juba teadaolevad kvantarvud, Z - tuumalaeng ning funktsioon -Laguerre'i kaaspolünoom. Molekulide arvutustel pole aga vesinikusarnased orbitalid praktiliselt rakendust leidnud ja seda järgmistel põhjustel:

a) suure osa vastavast täielikust baasist hõlmab pidevale spektrile vastav osa, mille arvestamine molekulide arvutustes on väga raske;

b) järjestikused vesinikusarnased orbitalid muutuvad kiiresti hajusateks (difuusseteks), mistõttu nende panus keemilise sideme energiasse kahaneb väga kiiresti;

c) elektronide tõukumise molekulaarintegraalid

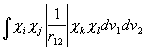
(3. 65)

on tehniliselt väga raskesti arvutatavad.

2. Slateri orbitalid (STO).

J.C. Slateri soovitusel (1930) võib vesinikusarnaste orbitalide asemel baasis kasutada lihtsustatud funktsioone

,

(3. 66)

kus Laguerre'i kaaspolünoom on asendatud lihtsa astmefunktsiooniga. Eksponendis olev kordaja määratakse valemist

,

(3. 67)

kus Z on tuumalaeng, S - varjestuskonstant ning efektiive peakvantarv. Esimese kolme perioodi elementide korral on viimane võrdne tõelise peakvantarvuga antud orbitalile. Varjestuskonstandid S võib leida vastavalt Slateri reeglitele:

a) arvesse tuleb varjestus vaid antud orbitalist madalamal asuvate elektronkihtide ning samas elektronkihis olevate elektronide poolt;

b) elektronid on jaotatud seejuures järgmistesse kihtidesse: jne.;

c) varjestuskonstant S = 0,35 iga elektroni jaoks samas kihis;

d) -kihtide jaoks on S = 0,85 igale elektroni kohta vahetult eelmises kihis ning S = 1,0 iga veelgi seespool asuva elektronkihi elektroni kohta;

e) -kihtide jaoks on S = 1,0 iga sisemise kihi elektroni kohta.

Viimasel ajal on hakatud rohkem kasutama STO-sid, mille eksponent-kordaja on optimeeritud kas aatomite või lihtsamate molekulide SCF arvutustest. STO-d annavad aatomi lainefunktsioonile hea kirjelduse tuumade ligiduses või siis suurel kaugusel neist. Seetõttu sobib STO-baasi kasutamine elektronide omaduste arvutamiseks aatomituumal või siis molekulidevahelise vastasmõju uurimiseks.

Tuleb silmas pidada, et STO-d on mitteortogonaalsed ning molekulide arvutuses on vaja tegeliku baasina kasutada lineaarkombinatsioone STO-dest. teiseks puuduseks, mis piirab STO- baasi laiemat kasutamist, on jällegi kaheelektroonsete integraalide (3.65) arvutamise keerukus. Muutujate mitteeraldatavuse tõttu ei ole intgreerimine praktiliselt teostatav riastkoordinaatides ning kasutada tuleb spetsiaalset sferoidaalset koordinaatsüsteemi. Kuid ka viimasel juhul võib integraali arvutamisel tegemist olla halvasti koonduvate lõpmatute ridadega.

3. Gaussi orbitalid (GTO).

Gaussi orbitalide e. Gaussi tüüpi funktsioonide (GTF) radiaalosa üldkuju on järgmine:

,

(3. 68)

kus on normeerimiskordaja ning mingi eksponentkordaja. Valemiga (3.68) on esitatud nn. sfääriline GTF, kuid kvantkeemilistes arvutustes on rakendust leidnud ka mõningad teist tüüpi GTF-d (Cartesiuse GTF, Hermite'i GTF jne.). Oluline on nende kõigi korral elektroni raadiuskoordinaadi ruudu kasutamine eksponendis, mis väga suurel määral lihtsustab molekulaar-integraalide arvutamist. Nimelt on GTF-de korral võimalik lihtne muutujate eraldamine juba ristkoordinaatides. Samas aga AO esitamine GTF-ga märksa ebatäpsem kui H-sarnase orbitali või STO-ga, kuna ta vastab üheelektroonse Schrödingeri võrrandi lahendile potentsiaali

(3. 69)

korral, mis erineb ilmselt palju tsentraalvälja potentsiaalist. Seetõttu on sama täpsuse saavutamiseks vaja kasutada rohkem GTF-e võrreldes STO-dega.

AO-de esituse leidmist GTF baasil võib teostada mitmel viisil;

1) SCF meetodil lahendatakse aatomi ülesanne, kusjuures AO-sid otsitakse GTF-na või lineaarkombinatsioonina GTF-dest:

(3. 70)

Variatsiooniparameetriteks on eksponentkordajad ja kordajad . Saadud baasifunktsioonide komplekti nimetatakse aatomoptimeeritud baasiks. Molekulide arvutustes võib kasutada ka otseselt saadud nn. primitiivseid funktsioone , arvestamata rittaarenduse (3.70) kordajaid .

Lihtsamate molekulide korral on võimalik reoptimeerida ka primitiivsete funktsioonide eksponendinäitajaid . Sel juhul on tegemist molekuloptimeeritud baasiga.

3) GTF baasil võib ritta arendada STO-sid;

.

(3. 71)

Vastavaid aatombaase tähistatakse STO-NG, kus N on GTF arv rittaarenduses (3.71). Eksponendinäitajad ja kordajad leitakse mittelineaarsete vähimruutude meetodil.

4) DZ-taseme täpsuse sissetoomiseks GTF korral kasutatakse nn. lõhestatud valentsbaasi, milles sisekihtide orbitalid on esitatud minimaalsele baasile vastavate AO-dega, valentskihi orbitalid aga kahe sama sümmeetriaga, kuid erineva eksponendinäitajaga orbitali kombinatsioonina, näiteks H aatomil

.

(3. 72)

Seda tüüpi baasiks on näiteks N-31G, kus N tähistab sisekihi orbitalide kirjeldamiseks kasutatud primitiivsete GTF-de arvu. 31G (lugeda kolm-üks-G) märgib seda, et valentskihi orbitalid on esitatud kahe orbitali kombinatsioonina, millest üks koosneb kolmest, teine aga ühest primitiivsest GTF-st:

.

(3. 73)

Kordajad ei muudeta molekulide arvutuste käigus. Sama kihi s- ja p-orbitalide jaoks kasutatakse samu eksponendinäitajaid .

5) Ka GTF baasi korral võib antud elemendi aatomile sisse tuua polarisatsioonifunktsioonid. Vastavate baaside tähistustes on see asjaolu märgistatud tärnikestega tähe G järel. Seega on polarisatsioonifunktsioone sisaldavaks baasiks näiteks 6-31G*.

Olgu elektronide arv süsteemis siis 2n. Molekuli lainefunktsioon on IPM lähenduses esitatav ühe Slateri determinandina. Kasutame viimase üleskirjutamiseks permutatsioonioperaatorit , mille toimel vahetuvad kahe elektroni koordinaadid molekuli lainefunktsioonis. Siis

,

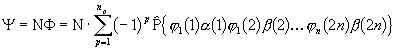(3. 74)

kus N on normeerimiskordaja ja ! - võimalike permutatsioonide üldarv. Lainefunktsioonis kasutatud molekulaarorbitalid olgu ortonormeeritud, s.t.

(3. 75)

1) Esmalt leiame normeerimiskordaja N väärtuse.

Tingimusest

(3. 76)

saame, et

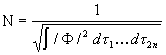
(3. 77)

Seega tuleb N leidmiseks arvutada integraal

(3. 78)

Integreerimine toimub siin nii üle elektronide ruumi-, kui ka spinnkoordinaatide (). Viimase avaldise lähemal vaatlusel ilmneb, et tegemist on integraalide summaga, millest iga liige esitab 2n vaid ühe elektroni koordinaatidest sõltuva integraali korrutist. Selles summas on põhimõtteliselt kahte tüüpi liikmeid:

a) . Siis esineb vähemalt kaks elektroni, mille spinn- või ruumikoordinaadid kuuluvad permutatsioonidele ja vastavates lainefunktsioonides esinevatele spinnorbitalidele. Orbitalide ortogonaalsuse tingimusest tuleneb siis, et

(3. 79a)

või

.

(3.79b)

Järelikult on kogu permutatsioonidele vastav liige summas (3.78) võrdne nulliga.

b) . Sel juhul on kõigil spinnorbitalidel nii kui ka korral samad elektronid ning järelikult

(3. 80)

Kuna ka , juhul kui , siis vastav liige summas (3.78) on võrdne ühega. Selliseid integraale, kus , on summas (3.78) kokku aga võrdselt permutatsioonide arvuga . Seega lõplikult

!

(3. 81)

ning vastavalt valemile (3.77):

(3. 82)

2) Alustame nüüd energia leidmist vastavalt keskväärtusteoreemile. Normeeritud lainefunktsiooni kasutades on

(3. 83)

Mitme elektroni süsteemi korral on Hamiltoni operaator jaotatav üheelektroonseks osaks ja kaheelektroonseks osaks :

,

(3. 84)

kus

(3. 85a)

koosneb nn. tüve hamiltoniaanidest iga osakese jaoks

(3.85b)

ning

(3. 86)

sisaldab üksnes elektronide vastastikuse elektrostaatilise tõukumise operaatoreid .

Kuna energia operaator on hermiitne, siis kehtib tema jaoks summa assotsiatiivsuse seadus ning me võime kirjutada:

.

(3. 87)

Edasi võime eraldi leida üheelektroonse energia

(3. 88)

ja kaheelektroonse energia

(3. 89)

väärtuse.

3) Üheelektroonse energia keskväärtus on vastavalt hamiltoniaanile (3.85a) vaadeldav summana üksikute elektronide üheelektroonsetest energiatest:

(3. 90)

Elektronide eristamatuse tõttu peab neist igaühe jaoks saadava energia keskväärtus olema sama. Seega piisab ainult esimese elektroni operaatorile vastava energia keskväärtuse leidmisest ning

(3. 91)

Asendades molekuli lainefunktsiooni normeeritud kujul viimasesse avaldisesse, saame

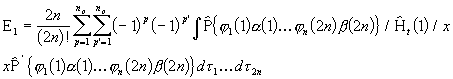
(3. 92)

Viimases summas on kahte tüüpi liikmeid. Esiteks

(3. 93a)

ja teiseks

(3.93b)

Suurus kujutab endast jällegi kattumisintegraalide korrutist üle üheelektroonsete orbitalide. Integraali korral on , kuna vähmalt ühe elektroni jaoks on kattumisintegraal

(3. 94)

s.o. selle elektroni jaoks, millele korral jäi järele orbital ning korral orbital . Seega on ka

.

Integraal (3.93a) on erinev nullist vaid juhul, kui , vastasel korral ei ole kattumisintegraalide korrutises kahe elektroni koordinaadid ja korral vastavad samadele spinnorbitalidele.

Tähistades

(3. 95)

saame, et

Kombinatsioone, kus ja , on ilmselt

tükki. Kuna integraal ei ole sõltuv spinnkoordinaadist, siis

nii selle spinnorbitali korral, kus i-s ruumiorbital on korrutatud spinni -funktsiooniga, kui ka juhul kui korrutis on spinni -funktsiooniga. Seega on kokku summas (3.92) integraali ning

(3. 96)

mis ongi üheelektroonse energia avaldiseks IPM lähenduses MO meetodis.

4) Siirdume nüüd kaheelektroonse panuse arvutamisele koguenergiasse. Elektronide eristamatuse tõttu on integraalis

(3.89)

sama väärtust omavat liiget. Järelikult võib vaadelda 1. ja 2. elektroni vahelist tõukumist ning

(3. 97)

Spinnorbitalide ortogonaalsuse tõttu on viimases kahekordses summas nulliga võrdsed kõik liikmed, välja arvatud juhtudel:

a) ;

b) , kuid vahetatud on just 1. ja 2. elektroni koordinadid.

Vaatleme neid juhtusid eraldi, kusjuures

(3. 98)

Kui , siis on võimalikud permutatsiooni iga elektronide 1. ja 2. konkreetse paigutuse korral spinnorbitalidele. Kuna aga operaator mõjub ainult lainefunktsiooni ruumilisele osale, siis elektronide 1. ja 2. spinni vastastikune orientatsioon on suvaline. Võimalikud on järgmised 4 kombinatsiooni: . Kui elektronid on erinevatel ruumiorbitalidel , siis on lubatud kõik nimetatud kombinatsioonid. Kui elektronid asuvad aga samal ruumiorbitalil, on vastavalt Pauli printsiibile lainefunktsioonis lubatavad ainult kaks viimast spinnfunktsioonide kombinatsiooni. Seega on iga ruumiorbitalide paari (i, j) korral energias liiget

(3. 99a)

ja liiget

.

(3.99b)

Kogu vastav panus energiasse on valemi (3.97) alusel:

(3. 100)

Seda energiat nimetatakse kuloniliseks energiaks ning ta väljendab elektronide vastastikuse elektrostaatilise tõukumise energiat. Integraale nimetatakse kulonilisteks integraalideks.

Kui valemis (3.97) , nii et vahetatud on ainult 1. ja 2. elektroni koordinaadid, on erinevatele permutatsioonidele vastavates lainefunktsioonides võimalikud järgmised neli 1. ja 2. elektroni spinnorbitalide kombinatsiooni:

Kolmandale ja neljandale reale vastavad liikmed summas (3.97) on võrdsed nulliga, kuna integreerimine üle spinnfunktsioonide annab

(3. 101)

Esimene ja neljas kombinatsioon annavad vastavalt ülejäänud elektronide permutatsioonide arvule kokku integraali

(3. 102)

Kuna kogu permutatsioonide arv oli operaatorite korral ühe võrra erinev, siis

ning integraalid lähevad koguenergia avaldisse (3.97) negatiivsete väärtustena;

(3. 103)

Vastav energia kannab vahetusenergia nime, integraale nimetatakse aga vahetusintegraalideks. Vahetusenergia on formaalselt molekuli stabiliseeriv. Sisuliselt arvestab ta lainefunktsiooni antisümmeetriast tingitud parandust elektronide tõukumisenergiale. Kuloniline energia on ülehinnatud, kuna tegelikult kaks paralleelse spinniga elektroni ei saa olla samas ruumipunktis üheaegselt. Integraalis on arvestatud aga ka selliseid konfiguratsioone nullist erineva lõpliku tõenäosusega.

Lõppkokkuvõttes on elektronide koguenergia molekulis IPM lähenduses:

,

(3. 104)

e. arvestades matemaatilist samasust

(3. 105)

Viimane avaldis ongi lähtevalemiks molekuli koguenergia leidmisel SCF LCAO MO meetodiga.

§ 10. Hartree-Focki meetod molekulaarorbitalide leidmiseks

Eelmises paragrahvis toodud avaldisest (3.105) võib arvutada molekuli elektroonse koguenergia eeldusel, et molekuli üheelektroonsed orbitalid e. molekulaarorbitalid on teada. Viimased tuleb aga enne leida vastavalt variatsiooniprintsiibile energia keskväärtusteoreemist. Integrodiferentsiaal-võrrandite süsteemi selle probleemi lahendamiseks tuletas V. Fock (1930) D.R. Hartree varasema töö (1928) põhjal, mistõttu see lähenemine kannab ka Hartree-Focki meetodi nime.

Defineerime kõigepealt kulonilise ja vahetusoperaatori mõisted. Kuloniline operaator on antud järgmise integraalina:

(3. 106)

seega kuloniline integraal

(3. 107)

on avalduv ilmutatud kujul vaid ühe elektroni koordinaatide funktsioonina.

Vahetusoperaatori jaoks ei saa otseselt välja kirjutada matemaatiliselt analüütilist avaldist, kuid ta peab rahuldama tingimust:

(3. 108)

Elektronide koguenergia (3.105) on siis välja kirjutatav kujul

(3. 109)

kus on juba tuntud üheelektroonse tüve hamiltoniaani operaator (3.85b).

Varieerime nüüd orbitale väikese suuruse võrra, kusjuures vastav energia variatsioon olgu . Optimumis (energia miinimumis) on:

(3. 110)

Hartree-Focki orbitalide leidmiseks kasutatakse lisatingimusena MO-de ortonormeeritud nõuet, s.o.:

(3. 111)

millest

(3. 112)

Variatsioonivõrrandit (3.110) lisatingimusel (3.112) saab lahendada Lagrange'i määramatute kordajate meetodil, kusjuures optimaalsed MO-d leitakse võrrandi

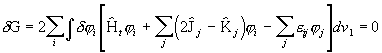
(3. 113)

lahenditena ( on määramatud kordajad). Kuna viimases avaldises on variatsioonid peavad nulliga võrduma nurksulgudes olevad avaldised. Vastavalt saame iga orbitali indeksi i korral kehtiva võrrandi

.

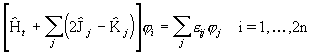(3. 114)

Need üheelektroonsed lainevõrrandid ongi Hartree-Focki võrrandid molekuli orbitalide leidmiseks. Nurksulgudes olev avaldis

(3. 115)

kannab Focki operaatori e. fokiaani nime.

Üheelektroonseid võrrandeid (3.114) lähemalt vaadeldes selgub, et i-nda MO leidmiseks on vaja teada teisi MO-sid , kuna neist sõltuvad operaatorid ning samuti on võrrandite paremal poolel ilmutatud kujul MO-de lineaarkombinatsioon. Seetõttu on Hartree-Focki võrrandite lahendamine võimalik vaid iteratsiooniliselt. Lähtuda tuleb mingist MO-de alglähendite komplektist . Seejärel on vaja arvutada neile algtähenditele vastavad kulonilised ja vahetusoperaatorid ning lahendada integrodiferentsiaalvõrrandite süsteem (3.114). Saadud orbitalidest moodustatakse uuesti Focki operaator ning korratakse protseduuri seni, kuni kahel järjestikusel iteratsioonisammul jäävad MO-d praktiliselt muutumatuks. Niisugune MO-de leidmine kannab veel kooskõlalise välja meetodi nime (SCF MO).

,

(3. 116)

kus on teisendusele vastava maatriksi elemendid. Üldjuhul on võimalik leida selline unitaarne teisendus, mille korral Hartree-Focki võrrandites on nullist erinevad vaid Lagrange'i kordajate maatriksi diagonaalelemendid, s.t.:

(3. 117)

Sel juhul on Hartree-Focki võrrandid (3.114) ümber kirjutatavad juba päris harilike üheelektroonsete Schrödingeri võrranditena:

(3. 118)

Tingimusel (3.117) leitud MO-sid nimetatakse kanoonilisteks molekulaarorbitalideks. Viimased ongi lõppresultaadiks enemikus standardsetes SCF MO meetodit realiseerivates arvutusprogrammides. Suurused vastavad elektroni energiale antud MO-l ning neid nimetatakse ka MO energiateks. Ilmselt ei ole molekuli koguenergia aga lihtne MO energiate summa, kuna iga elektroni energias on arvestatud tema interaktsioon teiste elektronidega, mis seetõttu tuleb -de summas arvesse kahekordselt. Seega molekuli elektroonne koguenergia avaldub järgmiselt

(3. 119)

Kanoonilised MO-d vastavad molekuli spektroskoopilisele olekule, kuid pole tingimata parimaks kirjelduseks laengujaotusele molekulis.

LCAO MO meetodis esitatakse molekuli lainefunkstioon ühe Slateri determinandina

(3. 120)

kusjuures üheelektroonsed molekuli orbitalid e. MO-d on esitatud lineaarkombinatsioonina teadaolevatest aatomorbitalidest (vt. § 8):

(3. 121)

Süstemaatilise meetodi MO-de leidmiseks sellisel kujul (SCF LCAO MO) esitasid sõltumatult C.C. Roothaan ja G.G. Hall (1951).

Rittaarenduse (3.121) asendamisel molekuli elektroonse energia integraalidesse saadakse:

(3. 122a)

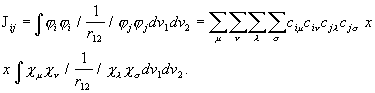
(3.122b)

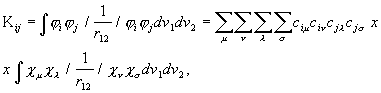
(3.122c)

kus

(3. 123a)

on tüve hamiltoniaani integraal,

(3.123b)

kuloline integraal ning

(3.123c)

vahetusintegraal AO-de baasil.

Defineerides tiheduse maatriksi elemendid, kui

(3. 124)

(summeerimine on teostatud üle elektroonpaaridega täidetud MO-de), saame elektroonse koguenergia avaldiseks:

.

(3. 125)

Kuna molekulaarintegraalide (3.123) väärtused on AO-de baasil arvuliselt leitavad, siis jäävad tundmatuteks suurusteks energia avaldises vaid MO-de kordajad .

Viimaste leidmiseks kasutatakse Roothaani-Halli meetodis jällegi kooskõlalise välja protseduuri. Koguenergia optimumi tingimusest

(3. 126)

tuleneb järgmine algebraliste võrrandite süsteem:

(3. 127)

kus

(3. 128)

on Focki maatriksi elemendid AO-de baasil ning

(3. 129)

AO-de kattumisintegraalid.

Lahendite ja kooskõlaliseks leidmiseks lähtutakse mingist alglähendite komplektist MO kordajatele . Harilikult vastavad need isoleeritud aatomite mudelile, s.t. igale MO-le vastab üks AO ja

.

(3. 130)

Lähtudes neist kordajatest, leitakse tiheduse maatriksi elemendid ning teadaolevaid molekulaarintegraale kasutades ka Focki maatriksi elemendid . Rõhutame siinkohal, et fikseeritud tuumade asendiga molekuli ülesande korral on molekulaarintegraale vaja arvutada vaid üks kord, mis on oluline arvutusteks kuluva aja kokkuhoiu seisukohalt. Edasi lahendatakse Roothaani-Halli võrrandid (3.127) ning saadakse uued kordajad ja energiad . Protseduuri korratakse seni, kui kas koefitsientide või koguenergia E väärtus jääb praktiliselt muutumatuks (vt. joonis 19a) . Võib esineda juhtumeid, kus koonduvust aga ei saavutata (joonis 19b) Enamasti on siis tegemist halvasti valitud baasiga, molekuli tasakaalulisest geomeetriast kauge tuumade konfiguratsiooniga või siis suurte muutustega tiheduse maatriksis järjestikustel iteratsioonisammudel.

Molekuli koguenergia koondumine SCF LCAO MO meetodil.

Molekuli orbitale klassifitseeritakse MO energiate järgi järgmiselt:

1) kui on tegemist molekuli stabiliseerivate e. siduvate MO-dega;

2) kui on tegemist molekuli seoseenergiat mittemuuvate, mittesiduvate MO-dega;

3) kui on tegemist molekuli lõhustavate e. lõdvendavate MO-dega.

Avatud elektronkihtidega molekulides on tegemist ühe või mitme mittepaardunud spinniga elektroniga. Eelnevalt vaadeldud Hartree-Focki ja Roothaani-Halli meetodid eeldasid aga paarisarvu elektronide olemasolu molekulis. Seetõttu on avatud kihtidega molekulide kvantkeemilisel arvutusel kasutada spetsiaalseid meetodeid. Laiemat kasutamist on leidnud siin kaks lähenemisviisi.

1. Piiratud Hartree-Focki meetod (RHF).

MO-de jaotus RHF meetodi korral.

Selle meetodi korral jaotatakse leitavad MO-d kahte ossa sõltuvalt nende täidetusest elektronidega. 0 või 2 elektroniga täidetud MO-d moodustavad suletud kihtidega orbitalide komplekti ning paardumata elektroniga orbitalid avatud kihtidega orbitalide komplekti . Kummagi komplekti jaoks lahendatakse eraldi Hartree-Focki võrrandid:

(3. 131a)

ja

.

(3.131b)

Märgime ära, et Focki operaatorid on erinevad, mistõttu erinevad on ka saadud lahendite komplektid. Molekuli elektroonne koguenergia arvutatakse vastavalt valemile

(3. 132)

kus on paardunud spinniga elektronide arv ning - elektronide koguarv.

2. Mittepiiratud Hartree-Focki meetod (UHF).

UHF korral vaadeldakse eraldi komplektidena molekulis esinevaid spinne omavate elektronide MO-sid. -spinniga elektronidele vastab MO-de kogum ning -spinniga elektronidele kogum (vt. joonis 21).

MO-de jaotus UHF meetodi korral.

Molekuli kogulainefunktsioon elektronidele on kahe Slateri determinandi korrutis, millest üks on koostatud MO-dest ja teine MO-dest :

(3. 133)

Molekulaarorbitalid leitakse kahe erineva Hartree-Focki võrrandi süsteemi lahendina:

(3. 134a)

ja

(3.134b)

kus Focki operaatorid on erineva kujuga.

Koguenergias

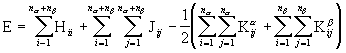
(3. 135)

on arvestatud seda, et vahetusintegraalid omavad nullist erinevaid väärtusi vaid paralleelsete spinnidega elektronide korral.

UHF meetodis pole enam ühedeterminantne molekuli kogulainefunktsiooni esitus, mistõttu koguenergia baasi suurendamisel ei koondu enam Hartree-Focki piirile (vt. § 10). Seega pole UHF meetodil leitud avatud kihtidega molekulide energiad otseselt võrreldavad harilikul RHF meetodil saadud suletud kihtidega molekulide energiatega. Nimetatud asjaolu tuleb kindlasti silmas pidada selliste protsesside kvantkeemilisel uurimisel, millest võtavad osa nii avatud kui ka suletud kihtidega molekulid.

UHF ja RHF meetodite võrdlusel avatud kihtidega molekulide jaoks tuleb märkida, et RHF meetodil saadud Lagrange'i kordajad ei ole siin interpreteeritavad orbitalide energiatena erinevalt suletud kihtidega molekulide arvutustest. Samuti ei anna RHF meetod õigeid spinni tihedusi, vaid lokaliseerib need ühele aatomile. Nii on RHF meetodil arvutatud spinnjaotus -radikaalis järgmine:

Märksa realistlikum on spinnjaotuse esitus saaduna UHF arvutustest:

Ka vastavad UHF meetodil saadud Langrange'i kordajad orbitalide energiatele (elektronide energiatele antud orbitalil) molekulis.

Vaatleme LCAO MO meetodi rakendust lihtsaima kaheaatomilise molekuli - -iooni korral. Lähtume minimaalsest baasist, s.t. kummalegi H aatomile on lokaliseeritud üks 1s-orbital. Viimased on siis esitatavad kujul

(3. 136)

MO kui nende kahe AO lineaarkombinatsioon on:

(3. 137)

Koefitsiendid võib ülesande korral leida lihtsatest sümmeetria põhimõtetest lähtudes. Kuna aatomituumad on ekvivalentsed, siis peab molekuli elektrontihedus mistahes punktis teatud kaugusel ühest aatomist olema võrdne tihedusega sümmeetriliselt samal kaugusel teisest aatomist asuvas punktis. See on võimalik vaid juhul, kui laengutiheduse avaldises

(3. 138)

on kordajad võrdsed:

(3. 139)

Viimast tingimust rahuldavad kaks lahendit koefitsientide jaoks:

(3. 140a)

ja

(3.140b)

Järelikult on minimaalset baasi rakendades -ioonil kaks võimalikku MO-d:

(3. 141a)

ja

(3.141b)

Koefitsiendid võib leida normeerimistingimusest

(3. 142)

millest

(3. 143a)

ja

(3.143b)

kus on kattumisuntegraal AO-de baasil.

MO-de kuju -ioonis.

Energia keskväärtuse elektronile neil MO-del võib leida, kui

.

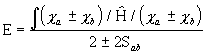(3. 144)

Vastavalt on korral

(3. 145a)

ja korral

(3.145b)

kus on energia integraalid. Nende integraalide ning -molekuli energia sõltuvus tuumadevahelisest kaugusest on toodud joonisel 23. Tasakaaluliste sidemepikkuste (dissotsiatsioonikõvera miinimumi) piirkonnas on MO korral molekuli energia negatiivsem (stabiliseeriv), võrreldes isoleeritud H aatomi ja prootoni energiaga. Tegemist on siduva MO-ga.

MO energia on positiivne aga kõigi sidemepikkuste korral. Seega on tegemist lõhustava MO-ga.

Molekulaarintegraalide ja energia sõltuvus tuumadevahelisest kaugusest -ioonis.

Vastavalt sideme pöördsümmeetriale nimetatakse molekulaarorbitale veel -orbitalideks. See mõiste on üldisem ning lähtub sellest, et keemilise sidemega seotud kahe aatomi AO-dest moodustatud MO võib välja kirjutada kujul:

(3. 146)

kus on keemilise sideme keskele tsentreeritud sfäärilised koordinaadid (vt. joonis 24).

Sfäärilised koordinaadid kaheaatomilises molekulis.

Seejuures on sideme ümber pöörlemise nurga funktsioon on

(3. 147)

Suurus on siin aatomite orbitaalse kvantarvuga l analoogne kvantarv, mille väärtus näitab MO nullpindade arvu, mis sisaldavad keemilise sidemega seotud aatomite vahelist sirglõiku. Juhul, kui , sõlmpinnad puuduvad ning tegemist on orbitalidega (analoogselt s-orbitalidega, kuid MO-de korral kasutatakse tähistena kreeka tähti).

Suuremate väärtuste korral on MO tähised samuti analoogsed AO-de tähistega:

-orbital tekib näiteks kahe -orbitali paralleelsel e. külgkattumisel. Selle MO nulltasandiks on -tasand, mis läbib ka keemilist sidet kujutavat sirglõiku (vt. joonis 25).

Mitteelektroonsete kaheaatomiliste molekulide MO struktuuri lihtsaks analüüsiks on sobiv kasutada järgmisi ligikaudseid reegleid:

-orbitali moodustumine.

1) kaks AO-d annavad olulise panuse samasse MO-sse vaid juhul, kui nende energiad isoleeritud aatomites on lähedased;

2) aatomorbitalid, mille kattumisintegraal on lähedane nullile, ei anna üheaegselt suurt panust samasse MO-sse;

3) sama sümmeetriaga MO-de, energiate sõltuvused ei lõiku sideme pikkuse muutudes.

Lähtudes neist reeglitest, vaatleme lähemalt MO-de diagrammi (joonis 26) homoaatomiliste kaheaatomiliste molekulide jaoks 2. perioodi elementidel.

Kõigepealt on vastavalt mõlema aatomi 1s-orbitalide kattumisele tekkinud siduv ning lõdvendav molekulaarorbital.

2. perioodi elementide homoaatomiliste kaheaatomiliste molekulide MO diagramm.

Nende orbitalide energiad on tunduvalt madalamal teise elektronkihi orbitalide kattumisel tekkinud MO-de energiast, kuid võrreldes isoleeritud aatomite 1s-nivoodega toimub -orbitalide energeetiline paigutus sümmeetriliselt. Niipalju kui muutub madalamaks 1-orbitali energia võrreldes 1s-nivooga, suureneb samuti -orbitali energia. Kuna 2. perioodi elementidel on 1s-orbitalid täidetud, siis on vastavalt molekulide elektronkihtide täitmise printsiibile elektronpaaridega asustatud nii - kui ka - MO. Summaarselt energeetiline efekt puudub, seega ei anna 1s -elektronid praktiliselt mingit panust keemilise sideme energiasse.

Aatomite ehitusest on teada, et 2s-AO on energeetiliselt märksa madalamal kui 2p-AO. Seega saadakse järgnevalt kahe 2s-AO kattumisel kaks MO-d: (siduv) ning (lõdvendav). Mõnevõrra keerulisem on kolme ekvivalentse p-orbitali kattumine vastastikku kahel aatomil. Olgu x-teljeks aatomituumi ühendav sirge. Siis -orbitalide kattumine toimub piki orbitalide telge ning saadud MO-d ei oma sideme telge (x-telge) läbivaid nulltasandeid (vt. joonis 27). Seega on tegemist -orbitalidega.

-orbitali moodustumine 2p-AO-dest.

Siduvaks on jällegi -orbital, lõdvendavaks aga orbital.

Sideme teljega risti olevad -ja -AO-d annavad kattudes aga kaks ühesuguse energiaga siduvat -orbitali ning kaks lõdvendavat -orbitali, mis on samuti energeetiliselt kõdunud. -orbitalide sümmeetria on toodud joonisel 28.

-orbitalide sümmeetria.

Lähtudes saadud MO-de diagrammist võib analüüsida kaheaatomiliste homoaatomiliste molekulide elektronstruktuuri seost nende mõningate omadustega (tabel 10).

Tabel 10

Kaheaatomiliste homoaatomiliste molekulide elektronstruktuur ja omadused

korral paigutuvad aatomite valentskihi kaks 2s-elektroni siduvale -le. Vastavalt sellele on molekul stabiilne ning teda on ka eksperimentaalselt tuvastatud (ca 1% lisandina) aurudes. Järgmisena tuleks vaatluse alla molekul. Tema neli valentskihi elektroni paigutuvad paarikaupa siduvale -le ning lõdvendavale -le. Kuna MO-de energeetiline paigutus on jällegi sümmeetriline, siis puudub molekulis summaarne siduv efekt ning ta pole püsiv. molekuli pole õnnestunud kindlaks teha ka eksperimentaalselt.

Tabelis 10 toodud andmetest võib täheldada otsest seost molekulides siduvatel MO-del asuvate elektronide ülejäägi ning nende stabiilsuse vahel. Mida rohkem on siduvaid elektrone, seda suurem on ka vastava sideme dissotsiatsioonienergia. Suurema orbitalide vastastikuse kattumise tõttu on siis lühem ka sideme pikkus molekulis.

Heteroaatomiliste kaheaatomiliste molekulide MO-de struktuuri analüüs on keerukam, kuna aatomite energeetiliste nivoode lõhenemine molekulis ei toimu enam sümmeetriliselt. Seetõttu on vajalik igal konkreetsel juhul teostada täielik kvantkeemiline SCF MO arvutus.

Molekulide Schrödingeri võrrandi lahendamist võib oluliselt lihtsustada nende sümmeetriaomaduste kasutamine. Arvestades molekulide sümmeetriat, võib nende MO-d transformeerida kujule, mille korral paljud molekulaarintegraalid jne. saavad võrdseks nulliga. See aga vähendab oluliselt reaalselt teostatavate arvutuste mahtu.

Molekulide korral võib sümmeetriaoperatsioone defineerida kui ???meetrilisi teisendusi, mille tulemusel molekul viiakse ekvivalentsesse asendisse võrreldes esialgsega, s.t. molekuli iga punkt kattub esialgse asendi ekvivalentse punktiga ( või iseendaga). Kvantkeemias defineeritakse sümmeetriaoperatsioone ka selliste matemaatiliste teisendustena, mis jätavad muutumatuks molekuli hamiltoniaani.

molekuli sümmeetria.

Lähtudes nende sümmeetriaelementide olemasolust, peab molekuli elektrontihedus punktides 1, 2, 3 ja 4 (vt. joonis 29) olema võrdne. Järelikult peab mistahes molekulaarorbitali korral olema rahuldatud tingimus:

(3. 148)

kus sulgudes on toodud ruumipunkti indeks.

MO-d ise peaks siis olema järgmiste omadustega

(3. 149)

Mitte kõik võimalikud 8 kombinatsiooni lainefunktsiooni märkidest ei realiseeru tegelikkuses, kuna näiteks operatsioon eeldab, et kui

siis ka

(pööramisel ).

Seega on lubatud kombinatsioonideks

(3. 150a)

ja

(3.150b)

Analoogiliselt saab tingimusest, kui

siis ka

lubatud kombinatsioonideks:

(3.150c)

ja

(3.150d)

Kokkusurutult võib neid seoseid välja kirjutada sümmeetria-operatsioonide mõjuna MO-dele. Kui kõik molekulile vastavad sümmetriaoperatsioonid jätavad lainefunktsiooni märgi muutumatuks, s.o.

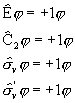
(3. 151)

siis on tegemist tingimusele (3.150a) vastava MO-ga. Analoogiliselt rahuldavad tingimusi (3.150b) sümmeetriaopratsioonide järgmised tulemused:

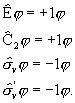
(3. 152)

Operaatorvõrrandite (3.151) ja (3.152) omaväärtusi +1 ja -1 nimetatakse ka karakteriteks. Antud molekuli MO-de sümmeetriat võibki iseloomustada tema karakterite tabeliga (vt. tabel 11).

Tabel 11

molekuli karakterite tabel.

Igale karakterite kombinatsioonile vastab spetsiaalne, antud MO-d tähistav indeks.

Karakterite tabelile vastav maatriks võimaldabki transformeerida MO-d sellisele kujule, kus paljud molekuli Focki maatriksi elemendid muutuvad nulliks. Kogu ülesande saab aga taandada mitme väiksema Focki maatriksi diagonaliseerimisele. Saadud MO-sid nimetatakse ka sümmeetria MO-deks.

Molekuli sümmeetriaoperatsioonid peavad rahuldama veel rida tingimusi:

1) mistahes kahe järjestikuse operatsiooni rakendamine peab olema samane mingi kolmanda sümmeetriaoperatsiooniga selles rühmas:

(3. 153)

kui ;

2) sümmeetriaoperatsioonid võivad kommuteeruda

(3. 154)

kuid nad võivad olla ka mittekommuteeruvad

(3. 155)

Näiteks püramiidse molekuli korral

(3. 156)

(vt. joonis 30);

3) mistahes sümmeetriaoperatsioonile peab rühmas vastama ka pöördoperatsioon , kusjuures

(3. 157)

kus on identsuse operatsioon.

Kahe sümmeetriaoperatsiooni järjestikune rakendamine molekulile.

4) rühmas olevate operatsioonide kogumeid, mis rahuldavad tingimusi 1-3, nimetatakse antud sümmeetriarühma alarühmadeks.

Molekuli sümmeetriarühma kindlakstegemiseks on oluline tunda veel punktrühmadesse kuuluvaid sümmeetriaoperatsioone. Tutvume mõningatega neist.

Teisendust molekuli sümmeetria keskpunkti suhtes nimetatakse inversiooniks ning tähistatakse . Peegeldus-pöördteisendus seisneb molekuli pööramises nurga võrra ning seejärel peegeldamises tasandis, mis on risti selle pöörde teljega. Peegeldustasand, mis sisaldab molekuli kõige kõrgemat järku pöördtelge e. peatelge, kannab vertikaalse peegeldustasandi nime ning teda tähistatakse . Peateljega risti olevat peegeldustasandit nimetatakse aga horisontaalseks tasandiks (tähistus ). Kui vertikaalne peegeldustasand jagab pooleks nurga kahe peateljega risti oleva teist järku telje vahel, on tegemist nn. dieedrilise tasandiga .

Sõltuvalt sümmeetria operatsioonide olemasolust sümmeteriarühmas jagatakse nad järgmistesse tüüpidesse.

1) - rühm. Molekulis on sümmeetria telg ning puuduvad teised sümmeetria elemendid. Näiteks

2) -rühm. Lisaks -teljele on molekulis n sümmeetriatasandit . Näiteks

3) -rühm. Lisaks -teljele on molekulis sümmeetriatasand . Näiteks trans-.

4) -rühm. Lisaks -teljele on molekulis temaga risti n 2. järku telge . Näiteks deformeeritud etüleen.

5)-rühm. Lisaks -rühma elementidel on molekulis sümmeetriatasand . näiteks .

6) -rühm. Lisaks -rühma elementidele on molekulis n sümmeetriatasandit . Näiteks trans-.

7) -rühm. Molekulis on ainult -telg, mis kuulub operatsiooni .

8) -rühm. Lineaarsed molekulid, mis ei oma -teljega risti olevat tasandit. Näiteks .

9) -rühm. Lineaarsed molekulid, mis omavad -teljega risti tasandi . Näiteks .

10) -rühm. Molekulil on sümmeetriatasand, kui puudub sümmeetriatelg. Näiteks

11) -rühm. Molekulil puuduvad sümmeetriteljed ja tasandid, kuid on sümmeetriatsenter.

12) -rühm. Molekul vastab tetraeedri sümeetriale. Näiteks .